DOI: 10.1557/opl.2012.1279

Graphene-Based All-Solid-State Supercapacitor with Ionic Liquid Gel Polymer Electrolyte

G. P. Pandey

and A. C. Rastogi

1,2

Center for Autonomous Solar Power (CASP),

Binghamton University, State University of New York, Binghamton, NY, 13902, USA

Department of Electrical and Computer Engineering,

Binghamton University, State University of New York, Binghamton, NY, 13902, USA

ABSTRACT

Graphene-based all-solid-state supercapacitors the using ionic liquid gel polymer

electrolyte have been fabricated and characterized. The gel polymer electrolyte has been

prepared by immobilizing ionic liquid 1-butyl-3-methylimidazolium tetrafluoroborate (BMIBF

)

with poly(vinylidene fluoride-hexafluoropropylene). Cyclic voltammetry studies show highly

capacitive behavior under fast scan rates. Impedance analysis show nominal charge transfer and

ion diffusion at pores related resistance contributions. The graphene-based solid-state

supercapacitor shows optimum capacitance of 80 mF cm

-2

(equivalent to the single electrode

specific capacitance of 76 F g

-1

). This corresponded to the specific energy of 7.4 Wh kg

-1

and

specific power of 4.5 kW kg

-1

. The supercapacitor cell shows stable cyclic performances for up

to 5000 cycles and possibly beyond.

INTRODUCTION

Electrical double layer capacitors (EDLCs) are the most studied class of supercapacitors

based on different kinds of porous carbon electrodes such as activated carbons, carbon

nanotubes, carbon xerogels, carbon nanofibers, carbide-derived carbons etc. [1-5]. In recent

years, graphene, two-dimensional layers of sp

-bonded carbon, has emerged as an extremely

promising electrode material for the next generation supercapacitors. Graphene possesses many

attractive properties such as high specific surface area up to 2675m

/g, excellent electrical

conductivity and remarkable mechanical stiffness [6].

Most of the graphene electrode based supercapacitors reported so far are based on the

liquid electrolytes (aqueous, organic and pure ionic liquid) [6-8]. There are many practical

limitations of the liquid electrolyte based devices such as leakage of electrolytes, bulky design,

corrosion of electrodes/cases of the devices, etc. The gel polymer electrolytes, generally prepared

by immobilizing liquid electrolyte in a host polymer matrix, offer a viable substitute for the

liquid electrolytes and they are being used for flexible and solid-state electrochemical devices,

e.g., batteries and supercapacitors. However, their poor thermal and electrochemical properties as

well as volatile organic constituents limit the performance characteristic of gel polymer

electrolytes [9]. Recently, room temperature ionic liquids (RTILs) have emerged as an attractive

alternative to the aprotic organic solvents due to their unique properties like excellent chemical

and thermal stability, nonvolatility and wider electrochemical potential window [10]. The ionic

liquid based gel polymer electrolytes have been used in various electrochemical applications

including rechargeable batteries and supercapacitors [5,10].

We have investigated electrochemical performance of the solid-state supercapacitors

comprising of identical graphene-based electrodes and the ionic liquid based gel polymer

electrolyte. Their specific capacitive and cyclic performance was evaluated by cyclic

voltammetry (CV) and galvanostatic charge-discharge techniques. Extensive impedance

spectroscopic studies were carried out to establish specific electrical attributes of the electrolyte

and electrode under various cyclic stages. The paper reports results of these studies and

demonstrates that the ionic liquid gel polymer electrolyte in combination with graphene electrode

offer excellent electrochemical performance of the solid-state supercapacitors.

EXPERIMENT

Graphene nanoplatelet (GNP) powder was purchased from Cheap Tubes Inc, having a

specific surface area ~700 m

-1

. GPNs have specifications of 4-5 layers, an average thickness

of 8 nm, and <2 µm average particle diameter. The GPNs were kept in a vacuum oven overnight

at ~100 °C prior to use. To prepare the electrodes, GPN powder was mixed with Poly(vinylidene

fluoride-hexafluoropropylene) (PVdF-HFP) binder on a ratio 90:10 (w/w) and formed as slurry

in acetone. This slurry was coated on to high density flexible graphite sheets (0.4 mm thick;

Fiber Materials Inc, USA), which also serve as current collectors. As prepared electrodes were

vacuum-dried overnight at ~100 °C before fabricating the supercapacitor cells. A solution cast

method was used to prepare the gel polymer electrolyte. PVdF-HFP, ionic liquid 1-butyl-3-

methylimidazolium tetrafluoroborate (BMIBF

) were purchased from Sigma-Aldrich. The ionic

liquid BMIBF

was vacuum-dried at 80°C for 24 h before use. The polymer PVdF-HFP was

separately dissolved in acetone. The ionic liquid BMIBF

was mixed with the PVdF-

HFP/acetone solution and stirred magnetically for 10 h. The weight ratio of the ionic liquid

BMIBF

to PVdF-HFP was kept at 80:20. The resulting viscous gel was used as polymer

electrolyte to fabricate solid-state supercapacitor cells.

All solid-state supercapacitor cells were fabricated by spreading the ionic liquid gel

polymer electrolyte over the graphene electrodes and the acetone was allowed to evaporate. Two

identically processed such electrodes were placed over each other and pressed lightly to form the

complete cell. The gel polymer electrolyte also acts as a separator. Such a cell design using an

ionic liquid based gel electrolyte simplifies the fabrication process, reduces the thickness of the

device, and makes it compact, highly reliable, and free from liquid leakage. A significant

advantage of this cell fabrication process is the electrolyte is deeply and extensively filled within

the pores of electrodes forming a larger interfacial contact between the porous graphene

electrode and gel electrolyte.

The performance characteristics of the solid-state supercapacitor cells were evaluated

using various electrochemical techniques like ac impedance spectroscopy, cyclic voltammetry

(CV), galvanostatic charge-discharge and prolonged cyclic tests in the two-electrode system. The

impedance measurements were carried out using the Solartron impedance analyzer (Model:

1260) in the frequency range from 10 mHz to 100 kHz at a signal level of 10 mV. The value of

overall capacitance of the supercapacitor cells was evaluated using the expression,

C = -1/2πf.Z″ (1)

where f is the frequency and Z″ is the imaginary part of complex impedance at frequency f. The

specific capacitance values of single electrode were evaluated by multiplying the overall

capacitance by a factor of 2 and dividing it by the mass of a single active electrode material. The

cyclic voltammetry and charge-discharge measurements were performed using the Solartron

Electrochemical Interface (Model: 1287). The cyclic voltammetry was carried out at different

scan rates between a floating potential of -1.0 and 1.0 V. The specific capacitance values from

this technique were evaluated using the relation,

C = (i

+ |i

|)/2s (2)

where i

and i

are the anodic and cathodic current and s is the scan rate (ΔV/Δt).

The supercapacitor charge-discharge tests were performed under galvanostatic conditions

using different current density values in the potential range 0.05 to 1.5 V. The specific

capacitance was calculated from the discharge curves by using the equation,

= i.∆t/m.∆V (3)

where i is the constant discharge current, ∆t is the discharge time, m is the total mass of the

electrode and ∆V is the voltage drop upon discharging (excluding the IR drop). The important

parameters associated with the power sources e.g. specific energy (E) and specific power (P)

were calculated by using the equations E = ½.C

∆V

and P = ∆V

/4m.ESR, respectively.

The

coulombic efficiency ‘η’ was evaluated using the following relation,

η = t

100% (4)

where t

and t

are the charging and discharging times, respectively.

DISCUSSION

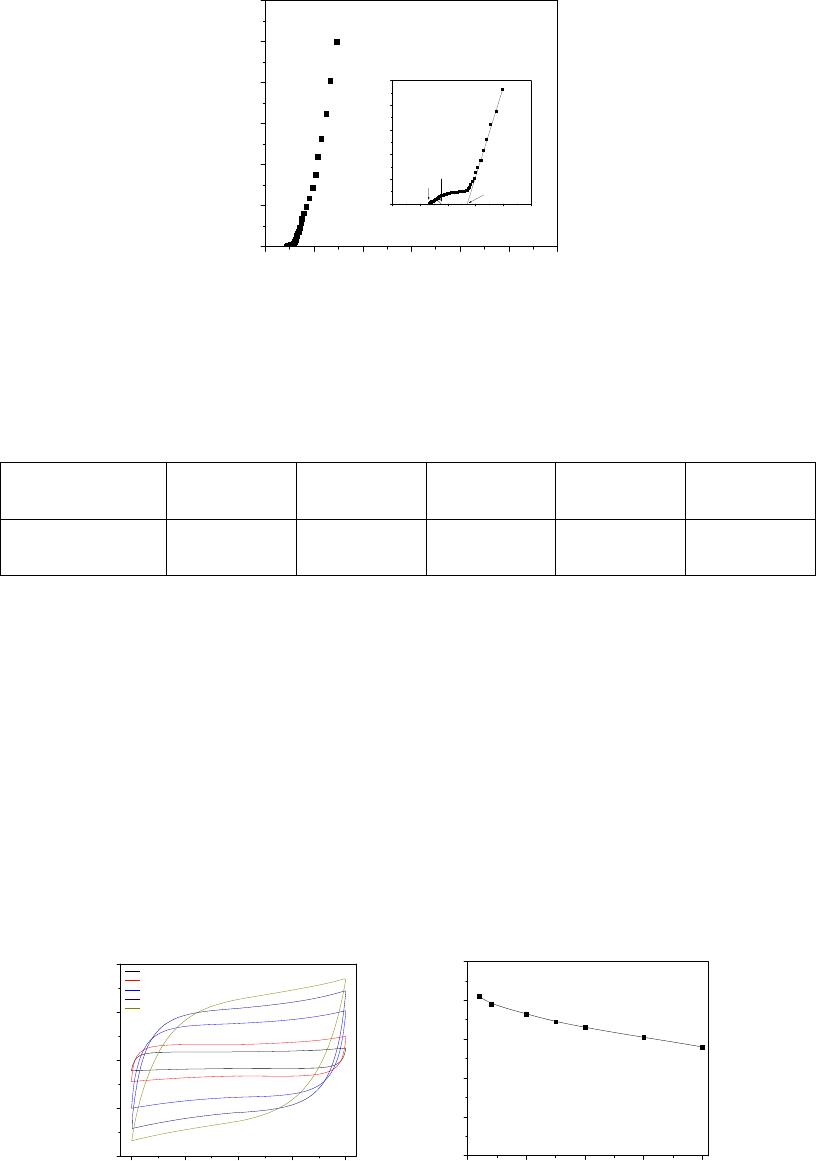
A typical impedance plot of the supercapacitor cell is shown in figure 1. The graphene

electrode in conjunction with the ionic liquid gel polymer electrolyte shows capacitive behavior

as reflected by the steep rising behavior of the impedance plot in the lower frequency region.

Various useful electrochemical informations can be extracted in different frequency regions. It is

known that an ideal impedance response for an ideal capacitor is a straight line parallel to the

imaginary axis of the complex impedance plot. The real capacitors, however, show a steep rising

capacitive impedance response in the low frequency region which is accompanied by high

frequency semicircular features owing to the bulk and interfacial properties. The expanded part

of the impedance response at higher frequencies (figure 1 inset) reflects the bulk properties of the

gel polymer electrolyte and the charge transfer process at the electrode-electrolyte interfaces.

The bulk resistance (R

) and interfacial charge-transfer resistance (R

) values of the capacitor

cell were easily evaluated from the intercept on the real axis of the impedance response. The

extrapolation for the low-frequency data gives another x-intercept equal to R

+ R

+ Ω, where Ω

represents one-third of ionic resistances in the pores for the distributed RC network of the

electrode in the pore. These resistances along with the capacitance values evaluated from

equation 1 at 10 mHz frequency are listed in Table 1.

0 20 40 60 80 100 120

-20

-40

-60

-80

-100

-120

Z" (Ω)

Z' (Ω)

10 mHz

6 8 10 12 14 16

-2

-4

-6

-8

-10

Z" (Ω)

Z' (Ω)

Figure 1. Typical impedance plot of solid-state supercapacitor cell recorded at room temperature

in the frequency ranging from 10 mHz to 100 kHz.

Table I. Electrical parameters of solid-state supercapacitor cell from the impedance analysis.

(Ω cm

)

(Ω cm

)

Ω

(Ω cm

)

(mF cm

-2

)

(F g

-1

)

Supercapacitor

cell

17.3 1.6 4.0 80 76

Overall cell capacitance at 10 mHz;

Singel electrode capacitance at 10 mHz

Figure 2(a) shows the cyclic voltammograms of the graphene| gel electrolyte |graphene

supercapacitor cell measured at different scan rates. The CV characteristics of the supercapacitor

cell show almost square shape and a nearly mirror image symmetry of the current response about

the zero current line irrespective of slow or fast scan rates. This indicates the capacitive behavior

of the cell with a double-layer formation at the porous interfaces. The specific capacitance values

of graphene electrode were calculated from the CV curves using equation 2. Figure 2(b) shows

specific capacitance as a function of the scan rates. After an initial decrease, the specific

capacitance values are almost stable, which confirm that the graphene electrodes based

supercapacitor could be cycled at high scan rates up to of 200 mV s

-1

without much degradation

in specific capacitance values.

-1.0 -0.5 0.0 0.5 1.0

-10

-5

Current (mA cm

-2

)

Voltage (V)

10 mV s

-1

20 mV s

-1

50 mV s

-1

75 mV s

-1

100 mV s

-1

(a)

0 50 100 150 200

100

(b)

Specific capacitance (F g

-1

)

Scan rate (mV s

-1

)

Figure 2. (a) CV curves of supercapacitor cell at different scan rates. (b) Variation in the

capacitance of graphene electrode as a function of the scan rates.

Figure 3(a) shows typical galvanostatic charge-discharge characteristics of the

supercapacitor cell at different current densities. The discharge characteristics for each current

density are linear, which further confirms the capacitive behavior of the supercapacitor cell. A

small sharp initial jump/drop in the voltage during the charging and discharging stages has been

observed. This arises from the ohmic loss across the internal resistance (R

), referred as ESR of

the cells. The internal resistance calculated from the voltage drops while discharging the cell is

typically 60 Ω cm

which is remarkably low considering the solid state design of the

supercapacitor under study. The discharge capacitance (C

) values have been evaluated from the

linear part of the discharge characteristics using equation 3. The specific capacitance values of

the graphene electrode calculated from charge-discharge curves are plotted as a function of

discharge current density in figure 3(b). Only a slight capacitance fading up to the current 5 mA

-2

has been observed, which indicates the suitability of this capacitor cell as power source. The

specific energy and specific power values of the supercapacitor were evaluated at a constant

current density of 1.0 mA cm

-2

. The graphene electrode shows a high capacitance value of 95 F

-1

and the corresponding specific energy of 7.4 Wh kg

-1

and specific power of 4.5 kW kg

-1

0 100 200 300

0.0

0.5

1.0

1.5

(a)

Cell Voltage (V)

Time (s)

1 mA cm

-2

2 mA cm

-2

3 mA cm

-2

012345

100

120

(b)

Specific Capacitance (F g

-1

)

Current Density (mA cm

-2

)

Figure 3. (a) Charge-discharge curves of the solid-state supercapacitor cell at different constant

current density. (b) Plot of specific capacitance as a function of discharge current density.

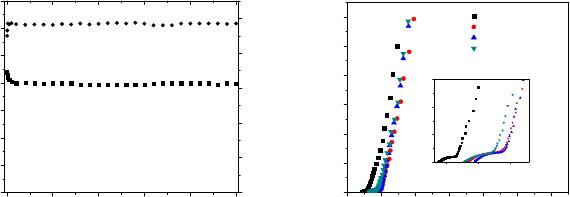
The cycling stability of the supercapacitors is important for practical applications. To

evaluate it for the symmetrical solid-state supercapacitor cells, we performed sequential

galvanostatic charge-discharge measurement at a constant current density of 1 mA cm

-2

. Figure

4(a) shows the variation in the discharge capacitance (C

) as a function of the charge-discharge

cycle numbers. The supercapacitor cell shows stable cyclic performance for over 5000 charge-

discharge cycles with only an initial ~10% fading in the capacitance. The coulombic efficiency

(η) of the charge-discharge process calculated using equation 4 is presented as a function of the

cycle number in figure 4(a). The charge/discharge efficiency gradually increases from ~93% in

first cycle to ~97% within an initial few cycles and then remains stable for up to 5,000 cycles. To

evaluate interfacial resistive parameters of the supercapacitor in the charge-discharge cycles, we

carried out impedance measurement at intermediate cycling stages. Figure 4(b) shows the

impedance plots of the supercapacitor test cell after 1500, 3500 and 5000 cycles. As evident

from inset view, after 1500 charge-discharge cycles, the ohmic resistance of the supercapacitor

increases slightly, apparently from a minor reduction in the electrical conduction property of the

gel polymer electrolyte. The low frequency region of the impedance plot related to the capacitive

behavior indicates a slight reduction in the capacitance during initial cycles but shows almost no

change on further cycling consistent with the specific data derived from cycling test.

0 1000 2000 3000 4000 5000

100

120

140

Cycle number

Discharge Capacitance (F g

-1

)

100

(a)

↵

Coulombic Efficiency (%)

0 20406080100120

-20

-40

-60

-80

-100

-120

(b)

Before cycling

after 1500 cycles

after 3500 cycles

after 5000 cycles

Z" (Ω)

Z' (Ω)

10 15 20

-5

-10

-15

Z" (Ω)

Z' (Ω )

Figure 4. (a) Variation in the discharge capacitance (C

) and coulombic efficiency (η) as a

function of the charge-discharge cycles at a constant current density of 1.0 mA cm

-2

. (b) Nyquist

plots of supercapacitor cell after certain number of charge-discharge cycles.

CONCLUSIONS

Graphene electrodes based all-solid-state supercapacitor using ionic liquid (BMIBF

) and

PVDF-HFP based gel polymer electrolyte have been fabricated and characterized. The maximum

overall capacitance value is observed to be 80 mF cm

-2

(equivalent to a single graphene electrode

specific capacitance of 76 F g

-1

). The specific energy ~7.4 Wh kg

-1

and the corresponding

specific power ~4.5 kW kg

-1

are realized in the solid state design. Highly stable charge-discharge

performance is demonstrated. Typically, supercapacitor cell shows ~90% capacitance retention

after 5000 charge-discharge cycles tested in this study. However, stable capacitance values

indicate nondegrading performance would extend to over 5000 cycles.

ACKNOWLEDGMENTS

This work was supported by the Office of Naval Research (ONR) grant to the CASP (Award

Number N00014-11-1-0658).

REFERENCES

1. B. E. Conway, Electrochemical Supercapacitors-Scientific Fundamentals and Technological

Applications, Kluwer Academic/Plenum Publishers, New York (1999).

2. E. Frackowiak and F. Beguin, Carbon 40, 1775 (2002).

3. P. Simon and Y. Gogotsi, Nat. Mater. 7, 845 (2008).

4. D. Qu and H. Shi, J. Power Sources 74, 99 (1998).

5. G. P. Pandey, S. A. Hashmi and Y. Kumar, J. Electrochem. Soc. 157, A105 (2010).

6. Y. Zhu, S. Murali, M. D. Stoller, K. J. Ganesh, W. Cai, P. J. Ferreira, A. Pirkle, R. M.

Wallace, K. A. Cychosz, M. Thommes, D. Su, E. A. Stach and R. S. Ruoff, Science 332, 1537

(2011).

7. C. Liu, Z. Yu, D. Neff, A. Zhamu and B. Z. Jang, Nano Lett. 10, 4863 (2010).

8. T. Y. Kim, H. W. Lee, M. Stoller, D. R. Dreyer, C. W. Bielawski, R. S. Ruoff and K. S. Suh,

ACS Nano 5, 436 (2011).

9. R. C. Agrawal and G. P. Pandey, J. Phys. D: Appl. Phys. 41, 223001 (2008).

10. M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater. 8, 621

(2009).