Chapter 11

Space Module On-Board Stowage

Optimization by Exploiting Empty

Container Volumes

Giorgio Fasano and Maria Chiara Vola

Abstract This chapter discusses a research activity recently carried out by Thales

Alenia Space, to support International Space Station (ISS) logistics. We investigate

the issue of adding a number of virtual items (i.e. items not given a priori) inside

partially loaded containers, in order to exploit the volume still available on board as

much as possible. Items already accommodated are supposed to be tetris-like,

while the additional virtual items are assumed to be parallelepipeds. A mixed-

integer non-linear programming (MINLP) model is introduced ﬁrst, then possible

linear (MILP) approximations are discussed, and a corresponding heuristic solution

approach is proposed. Guidelines for future research are highlighted, and experi-

mental insights are provided to show the efﬁciency of the proposed approach.

Keywords Space cargo accommodation • Container loading problem • Non-standard

three-dimensional packing • Virtual items • Tetris-like items • MINLP models

• MILP approximations • Heuristics

11.1 Introduction

This study has been motivated by the challenging issue of cargo accommodation in

space vehicles and modules. Speciﬁcally, we focus on the on-board stowage

problem of the International Space Station (ISS, http://www.nasa.gov) with partic-

ular reference to the European Columbus Laboratory (http://www.esa.int). The

laboratory also provides logistic support for the ISS (consult [6]).

G. Fasano (*)

Thales Alenia Space Italia S.p.A., Str. Antica di Collegno 253, 10146 Turin, Italy

e-mail: [email protected]

M.C. Vola

Altran Italia S.p.A., Turin, Italy

e-mail: [email protected]

G. Fasano and J.D. Pinte

r (eds.), Modeling and Optimization in Space Engineering,

Springer Optimization and Its Applications 73, DOI 10.1007/978-1-4614-4469-5_11,

Springer Science+Business Media New York 2013

249

A ﬂeet of vehicles is used for transportation, on the basis of the cargo plan

provided by NASA, to control the upload/download ﬂow logist ic to/from the ISS.

The cargo plan is supposed to be repeatedly updated over time, as the whole logistic

process continues. If not all planned upload cargo can be accommodated at a given

time, then part of it can be temporary crossed off the list and taken into account in

further launches.

To meet (at least approximately) a given cargo plan, a number of non-trivial

three-dimensional packing problems arise. Once the optimal packing solution

(that offers the best loading of the listed items) at the current step is obtained, the

cargo engineer is still asked to execute a further demanding job. How could the

residual space (volume) be suitably exploited? More precisely, we assume that it is

allowed, for each container not yet fully loaded, to add a certain number of virtual

items (that are not known a priori), by reallocating the ones already accommodated,

if necessary. What sort of virtual items could be properly added, in order to

maximize the loaded volume of each container? A further optimization process is

then performed, and possible “hole-ﬁlling” (virtual) items are suggested, thereby

making the achievement of further cargo planning objectives signiﬁcantly easier.

In this chapter we discuss the issue of optimizing the volume exploitation of a

partially loaded single container by adding up to a maximum number of virtual

items, repositioning, if necessary the objects already loaded. From the analytical

point of view, this problem is quite similar to the one consisting of creating internal

separation elements of ﬁlling material (such as foam), to protect the items

loaded inside the containers and to prevent their collision especially during the

launch phase.

Although our s tudy has originated in order to tackle the on-board stowage of

space modules, it can be applied also in many other contexts. Examples include

the use of autonomous robots in future space exploration ( e.g. to identify accessi-

bility zones and to support loading and assembling activities); another area—not

in the space engineering context—is that of the very large system integration

(VLSI).

The literature related to packing issues is extensive (consult, e.g. [3]). A major

subject area within this broad context is the orthogonal packing of two- and three-

dimensional objects inside convex domains (cf., e.g. [1, 7, 12, 13, 15]). A number of

mixed-integer (linear) programming (MILP) formulations of two- and three-

dimensional orthogonal packing problems are available (see, e.g. [2, 14 , 16]). The

topic discussed here extends a previous MIP-based approach (see [4]) devoted to

the three-dimensional packing of tetris-like items within a convex domain, in

presence of additional conditions. The term tetris-like refers either to

parallelepipeds or, more generally, to properly connected clusters of mutually

orthogonal parallelepipeds as illustrated by Fig. 11.1.

In the following discussion, we assume that the container is a convex domain.

Alreadyloadeditemsareassumedtobetetris-like, while the additional virtual

items are parallelepipeds of various sizes. Our objective is to create a number o f

virtual items (without exceeding a given bound) a nd to determine their sizes

so that the total loaded volume inside the c ontainer is maximized.

250 G. Fasano and M.C. Vola

The problem is stated in Sect. 11.2 . Section 11.3 formulates it in terms of mixed-

integer non-linear programming (MINLP) (consult, e.g. [8–11, 17, 18, 22]).

A simpliﬁed approach, based on MILP approximations, is discussed in Sect. 11.4.

A review of some real-world applications is given in Sect. 11.5, including the

discussion of a heuristic approach that has been quite efﬁcient in practice.

11.2 Problem Statement

To formulate the problem studied, we shall consider a convex domain D which is a

polyhedron (or it can be approximated by a polyhedron). Inside D, we have a set of

n tetris-like items (TLI), each one consisting of a cluster of mutually orthogonal

parallelepipeds, called components, see Fig. 11.1.

We shall also suppose that the TLIs have been positioned within D, in compli-

ance with the following packing rules:

• each TLI has to be positioned parallel to an axis of a pre-ﬁxed orthonormal

domain reference frame (orthogonality conditions);

• each TLI has to be contained within D (domain conditions);

• components of different TLIs cannot overlap (non-intersection conditions).

In particular, this means that at least a feasible solution to the orthogonal packing of

the given set of TLIs exists. We are then asked to add up to

N virtual items, consisting

of parallelepipeds with sides of variable length (but not less than a given minimal

threshold), so that the total volume occupied by the TLIs plus the virtual items

is maximized. We are not requested to keep the initial feasible solution for the TLIs,

i.e. we are allowed to move them by arbitrary feasible rotations and translations.

However, we must take into account the following rules for each virtual item (VI):

• each VI side has to be parallel to an axis of the pre-ﬁxed orthonormal domain

reference frame (orthogonality conditions);

Fig. 11.1 Tetris-like item

(two-dimensional

representation)

11 Space Module On‐Board Stowage Optimization by Exploiting Empty... 251

• each VI has to be contained within D (domain conditions);

• VIs cannot overlap with the packed TLIs or with other VIs (non-intersection

conditions).

11.3 An MINLP Model Formulation

A MINLP formulation of the outlined optimization problem is described next.

First of all, let us point out that the packing rules expressed in Sect. 11.2 can be

grouped as follows:

• orthogonality, domain and non-intersection conditions for TLIs only;

• orthogonality, domain and non-intersection conditions for VIs only;

• non-intersection conditions between TLIs and VIs.

The orthogonality, domain and non-intersection conditions for TLIs have been

discussed in detail in [4]. For the sake of completeness, we will brieﬂy discuss these

conditions here. An orthogonal main reference frame with origin O and axes w

b ∈ {1,2,3} is deﬁned, and a local reference frame is associated to each TLI. Each

local reference frame is chosen so that all TLI components lie within its ﬁrst

(positive) octant. Its origin coordinates, with respect to the main reference frame

axes, are denoted by o

. Next, we introduce the set O of all possible orthogonal

rotations, admissible for any TLI’s local reference frame, with respect to the main

one. Under the orthogonality assumptions there are 24 orthogonal rotations since

the TLIs are in general asymmetric objects.

For each TLI i, we introduce the set C

of its (parallelepiped) components. E

indicates, for each component h of TLI i, the set of the eight vertices associated to it,

and an extension of this set is obtained by adding to E

the geometrical centre of

component h. This extended set is denoted by E



and its generic element by

;  ¼ 0, in particular, represents the geometrical centre. For each TLI i and each

possible (orthogonal) orientation o ∈ O ¼ {1,...,24}, the binary variables W

2 0; 1

are deﬁned, with the mea ning: W

¼ 1 if TLI i has the orthogonal

orientation o ∈ O, and W

¼ 0 otherwis e.

The orthogonality conditions for TLIs (only) are expresse d as follows:

¼ 1; (11.1)

8b; 8i; 8h 2 C

; 8 2 E



; w

bhi

¼ o

obhi

; (11.2)

where w

bhi

are the vertex coordinates of component h or its geometrical centre,

relative to TLI i, with respect to the reference frame axes w

; W

obhi

are the

coordinate differences between points  2 E



and the origin of the local reference

252 G. Fasano and M.C. Vola

frame, with o

coordinates, projected alon g the w

axis of the main reference frame,

corresponding to the TLI i orientation o.

Next, the domain conditions for TLIs (only) are expressed as follows:

8b; 8i; 8h 2 C

; 8 2 E

bhi

ghi

; (11.3)

8i; 8h 2 C

; 8 2 E

ghi

¼ 1; (11.4)

where l

ghi

are non-negative variables; (V

),...,(V

) are the

vertices of D (whose coordinates, in the main reference frame, are assumed as

non-negative, without loss of generality).

The non-intersection conditions (again, for TLIs only) are represented by the

constraints below:

8b; 8i; 8j; i < j; 8h 2 C

; 8k 2 C

b0hi

 w

b0kj



obhi

þ L

obkj



 D

1  s

bhkij



;

(11.5.1)

8b; 8i; 8j; i < j; 8h 2 C

; 8k 2 C

b0kj

 w

b0hi



obhi

þ L

obkj



 D

1  s



bhkij



;

(11.5.2)

8i; 8j; i < j; 8h 2 C

; 8k 2 C

bhkij

þ s



bhkij



 1; (11.6)

where D

are the sides (parallel to the main reference frame axes) of the parallele-

piped of minimum volume that encloses D; w

b0hi

and w

b0hj

are the centre coordinates

of components h and k; L

obhi

and L

obkj

are their sides, parallel to the w

axis,

corresponding to the orientation o and s

bhkij

and s



bhkij

2f0; 1g. If either in (11.5.1)

or (11.5.2) a variable s is set to one, then the corresponding constraint is called a

relative position constraint.

Constraints (11.1)–(11.6) represent the necessary and sufﬁcient conditions for

placing the given n TLIs in compliance with the packing rules stated above and hold

when only TLIs are involved (constraints 11-6 can be expressed in terms of

equations, in order to make the model formulation tighter). The orthogonality,

domain and non-intersection conditions for VIs only, as well as the non-intersection

ones involving both TLIs and VIs, are formulated next.

As the number of VIs actually used may be smaller than the maximum allowable

N, the binary variable w

∈ {0,1}, j ∈ {1,...,N}, is introduced: w

¼1ifVIj is used,

and w

¼ 0 otherwise.

11 Space Module On‐Board Stowage Optimization by Exploiting Empty... 253

The orthogonality conditions for VIs are then implicitly stated by the following

domain conditions and hold for each vertex  of VI j:

8b; 8j; 8 2 E

bj

gj

; (11.7)

8j; 8 2 E

gj

¼ w

; (11.8)

where E

is the set of vertices associated to VI j and w

bj

are their coordinates; both

bj

and l

gj

are non-negative variables.

The following inequalities represent the non-intersection conditions between the

generic TLI i and VI j:

8b; 8i; 8j; 8h 2 C

b0hi

 w

b0j



obhi



 D

1  s

bhij



;

(11.9.1)

8b; 8i; 8j; 8h 2 C

b0j

 w

b0hi



obhi



 D

1  s



bhij



;

(11.9.2)

8i; 8j; 8h 2 C

bhij

þ s



bhij



¼ w

; (11.10)

where w

b0j

are the centre coordinates of VI j, l

the side parallel to the w

axis,

bhij

2f0; 1g and s



bhij

2f0; 1g are binary variables.

The condition s

bhij

¼ 1 implies that the side projection of h and j respectively do

not overlap along the w

axis and h precedes j, while s

bhij

¼ 0 makes the

corresponding non-i ntersection constraint redundant. An essentially identical con-

sideration holds for s



bhij

Analogous constraints are stated when dealing with the non-intersection

conditions relative to each pair of VIs:

8b; 8j; 8j

; j<j

b0j

 w

b0j



þ l



 D

1  s

bjj



; (11.11.1)

8b; 8j; 8j

; j<j

b0j

 w

b0j



þ l



 D

1  s



bjj



; (11.11.2)

8j; 8j

; j<j

bjj

þ s



bjj



 w

þ w

 1:

(11.12)

254 G. Fasano and M.C. Vola

The lower bound L is further introduced for all VI sides, in order to obtain valid

solutions from a practical point of view (since too small VIs would be useless),

together with additional upper bounds:

 l

 D

: (11.13)

The objective function to maximize is simply deﬁned by the total volume of the

VIs added:

max

()

: (11.14)

Remark 1 In [4], a number of additional conditions such as a given minimum gap

between items, the pre-ﬁxed position or orientation of some of them, the presence

of structural elements, forbidden zones (holes) inside the domain and separation

planes (movable within given ranges) have been taken into account. Such

conditions can be easily added to the model under consideration here; in fact,

such conditions are taken into account in some of the tests reported in Sect. 11.5).

Remark 2 As far as the balancing conditions are concerned , the concept expressed

in the previous work [4] could also be easily added to the present MINLP model by

associating to each (added) VI a constant (average) density r . The previous

balancing expressions are rewritten:

8g; c

0;

g¼1

¼m

i¼1

j¼1

g¼1



where

m ¼

i¼1

j¼1

Differently from the case discussed in [4], the above conditions are not linear.

Remark 3 The presence of the binary variable w

in the expressions (11.13)

guarantees that if a certain virtual item is not added, its contribution to the total

volume computation is zero.

11 Space Module On‐Board Stowage Optimization by Exploiting Empty... 255

11.4 MILP Model Approximations

The MINLP model formulated in Sect. 11.3 is (most likely) hard to solve to

optimality. A ﬁrst simple linear approximation is generated easily by adopting the

surrogate objective function below:

max

b;j

()

: (11.15)

An alternative approach consists of substituting the original objective function

(11.14) by a separable one. This can be easily achi eved by adopting the (equivalent)

objective function:

max

j;b

ln l

()

: (11.16)

A linear piece-wise approximation of each single-variable term then reduces the

original MINLP model to a much simpler (approximate) MILP (cf., e.g. [ 20 ]). A

straightforward formulation to obtain this can be achieved as follows (consult [21]).

For each b, we introduce an arbitrary partition A

; ...; A

; ...



of [ L; D

] and

then state the conditions

8b; 8jl

baj

; (11.17)

8b; 8j ln l



baj

ln A

; (11.18)

8b; 8j

baj

¼ w

; (11.19)

where, for each b and j, the l

variables are subject to the further SOS2 (special

ordered set of type 2, [21]) restriction: at most two consecutive l

baj

can be non-zero.

The objective function then becomes

max

a;b;j

baj

ln A

()

: (11.20)

Remark 4 The SOS2 restriction shown above can be tackled either algorithmically

or by introducing additional binary variables and proper constraints in the model

[19, 21]. If could also be seen that such restriction in our speciﬁc case could be

dropped tout court, but this is beyond the scope of the chapter.

256 G. Fasano and M.C. Vola

Remark 5 A further possibility of converting a sum of products into a separable

function could be considered [21]. In the case of the product of two variables q

is sufﬁcient to introdu ce new variables s

, by performing the transformation

ðq

þ q

Þ; s

ðq

 q

Þ;

and substituting q

with s

 s

. The method can be easily extended when the

products involve more than two variables and a linear piece-wise approximation of

the quadratic terms obtained can be achieved, as in the case of the logarithmic

functions discussed above.

Remark 6 The MILP approximations described in this section could well be

considered to provide a good starting solution to an MINLP solution process.

11.5 Practical Applications

On the basis of the MILP approximation relative to the surrogate objective function

11.15 mentioned in Sect. 11.4, a heuristic approach has been investigated to obtain

quick (satisfactory, but typically suboptimal) solutions to the original problem : this

approach will be reviewed next.

An appropriate lower bound, as stated by conditions (11 .13), is generated each

time, depending on the speciﬁc model instance analysed. In addition to this point, it

is recommended to get rid of solutions with strongly asymmetric, “non-cube-

shaped” VIs. (The surrogate objective function tends to give rise to such VIs, as

matter of fact.) Figure 11.2 illustrates an example with just three VIs. In the image

on the left no additional limitation was posed, unlike in the case shown on the right.

The heuristic approach proposed here poses further conditions on the possibility

of reallocating the already loaded TLIs. Whi le o rthogonal rotations of the TLIs are

allowed (except for the pre-oriented ones, if any), their translations are partially

restricted on the basis of the relative positions they already have (refer to constraints

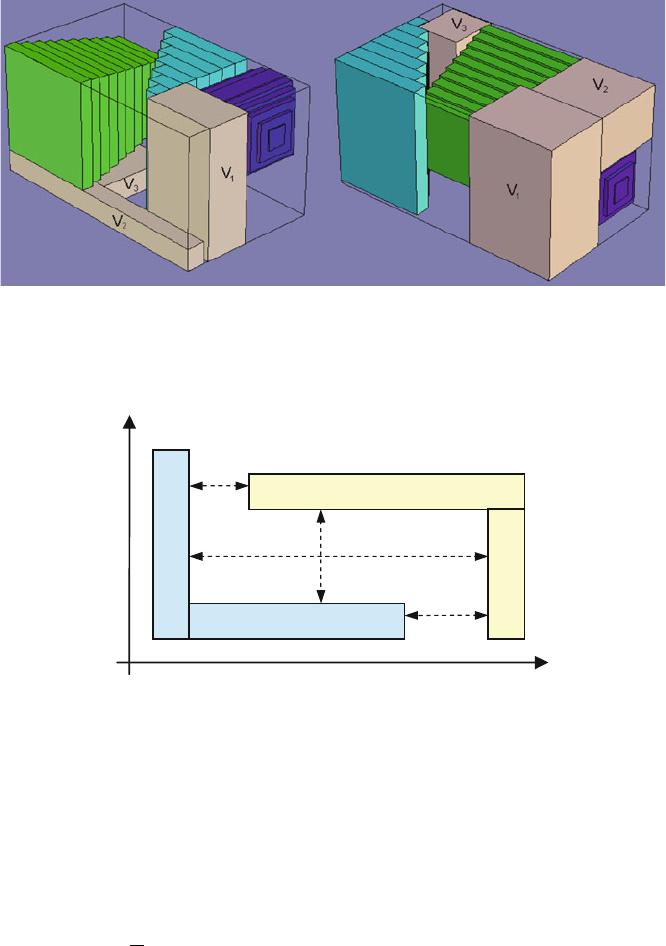
(11.5.1) and (11.5.2)). This restriction is linked to the concept of abstract conﬁgu-

ration [4, 5]: given a number of couples of components (belonging to different

TLIs) an abstract conﬁgur ation consists of a set of variables s set to one (one and

only one for each couple), so that, in any unbounded domain, the subspace

delimited by the corresponding non-intersection constraints is a feasible region

(see Fig. 11.3).

In the heuristic approach proposed here, as a ﬁrst step, an abstract conﬁguration

compliant with the solution of the already loaded TLIs is selected. This can be done

as suggested in [5]. The abstract conﬁguration is then imposed to the MILP model,

so that only the relative non-intersection constraints are considered, while all the

remaining ones are neglected. This gives rise to a reduced MILP model that

dramatically decreases the computational effort of the solution process.

11 Space Module On‐Board Stowage Optimization by Exploiting Empty... 257

Since the addition of several VIs all together would represent a signiﬁcant

computational job, the heuristic procedure proceeds, step by step, adding one VI

after the other, until a satisfactory solution is obtained or their maximum number is

reached. The heuristic proposed is based on the algorithm outlined here below.

Algorithm. Incremental introduction of virtual items

Input n tetris-like items, convex domain

Output tetris-like items repositioning, positions and dimensions of the added

virtual items (<

Begin

Generate an abstract conﬁguration corresponding to the given tetris-like item

accommodation;

j 0; //numer of virtual items

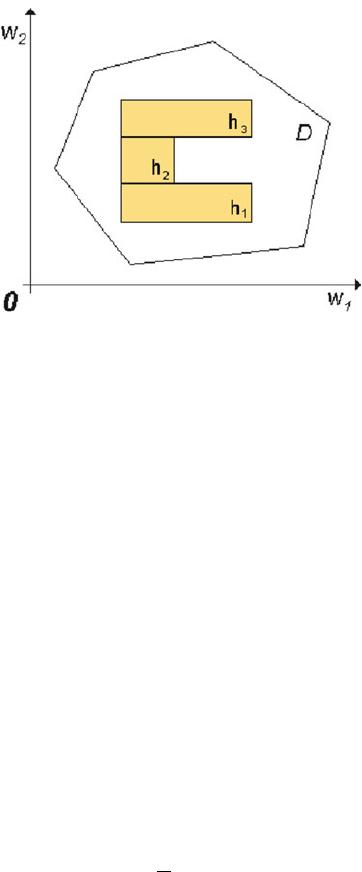
Fig. 11.2 Example of solutions without/with extra limitations: compare the left/right side

solutions shown

Fig. 11.3 Example of an abstract conﬁguration: two-dimensional representation

258 G. Fasano and M.C. Vola