A Band Structure Phase Diagram Calculation of 2D BiSb Films

Ming Y. Tang

and Mildred S. Dresselhaus

1,2

Department of Electrical Engineering and Computer Science,

Massachusetts Institute of Technology, Cambridge,

MA 02139, U.S.A.

Department of Physics, Massachusetts Institute of Technology,

Cambridge, MA 02139, U.S.A.

ABSTRACT

Ever since the birth of thermoelectrics, it has been well known that semiconductors

(materials with a relative small bandgap) give the best thermoelectric performance. From

quantum mechanics, it is also well known that low dimension quantum confinement leads to

changes in the band alignment of a material. Thus, a semimetallic material can be made

semiconducting by using low dimensionality quantum confinement effects. BiSb alloys have

been of particular interest for thermoelectric application in the temperature range of 70K to

100K. In bulk form, BiSb alloys can either be a semimetal or a semiconductor, depending on the

alloy composition. Moreover, semimetallic BiSb alloys can be made semiconducting by using

the low dimensionality quantum confinement concept. With these two previous concepts in

mind, it is valuable to further explore the dependence of the band alignment for different alloy

concentrations and different confinement conditions for BiSb alloys.

Following the study of the effect of the Sb concentration and of the wire diameter on the

semimetallic or semiconducting phase of BiSb alloy nanowires [1], we now examine the

corresponding effect of the Sb concentration and the film thickness on the properties of BiSb

alloy films. A band structure phase diagram is calculated, giving the details on the dependence

of the relative band edge position on the film thickness and the Sb concentration. This phase

diagram gives a first hand guideline for choosing the film thickness and the Sb concentration to

better improve the thermoelectric performance of BiSb alloy films.

INTRODUCTION

In the 1990s, using low dimensional physics concepts, Hicks and Dresselhaus predicted that

a dramatic enhancement in thermoelectric performance was possible through the use of quantum

wells and quantum wires [2, 3]. In the late 1990s, Chen also predicted that an enhancement in

ZT could result from the significant reduction in the thermal conductivity in a low dimensional

system [4]. At the same time, nano-fabrication technology rapidly improved during the last

decade. With advances in technology and in new low dimensional concepts, increases in the

thermoelectric figure of merit (

/( )

eph

ZT S T

κκ

=+ where

is the electrical conductivity, S is

the Seebeck coefficient,

and

are respectively the electrical and lattice thermal

conductivity, and T is the temperature) have been demonstrated [5].

Refrigeration is one of the major applications for thermoelectric materials. The advantage

of thermoelectric refrigeration is the absence of moving compressor units as is done using

conventional refrigerators. Thermoelectrics not only decrease the noise level and the weight of

the refrigerator, they also increase the refrigerator life cycle.

BiSb alloys have been of particular interest for thermoelectric refrigeration in the

temperature range of 70K to 100K. It has always been important for the research community to

have theoretical guidelines before working with thermoelectric materials for the desired

applications, because of the large number of variables that need to be considered in laboratory

demonstrations. Following the study of the dependence of the semimetallic or semiconducting

phase of BiSb alloys nanowires on Sb concentration and on wire diameter [1], this paper now

examines the corresponding effect of the Sb concentration and the film thickness on the

properties of BiSb alloy films. The results of this study give guidelines for choosing the film

thickness and the Sb concentration to improve the thermoelectric performance of BiSb alloy

films.

BACKGROUND

Bismuth (Bi)

Figure 1. Crystal structure (left) and Brillouin zone (right) of Bismuth. The dark gray near-

center Bi atom is displaced along the trigonal axis such that the distance between that Bi atom

and the bottom dark Bi atom is different than the distance between the near-center dark gray Bi

atom and the top dot-shaded Bi atom.

Bismuth (Bi) is a group V element and is a semimetal in bulk form. Bi is the most

diamagnetic of all metals, and its thermal conductivity is the 2

lowest among all metals, next to

that of mercury. Bi has a high electrical resistance and has the highest Hall effect of any metal

[6]. The crystal structure of Bi is rhombohedral with two atoms per unit cell. Its unit cell can be

described as a FCC unit cell stretched along the trigonal direction with a small displacement of

the near-center Bi atom from the central location (see Figure 1). Due to these two distortions,

the degeneracy at the L <111> points is lifted, and the T points [111,

111] are structurally

distinct from the 6 structurally equivalent L points [

111 , 111, 111, 111, 111, and 111 ] in the

distorted rhombohedral structure that describes Bi, Sb, and BiSb alloys (see Figure 1). In

crystalline bulk Bi, there is an overlap of 38meV between the conduction band at the L points

and the valence band at the T points. Bi is an anisotropic material with a ratio of greater than

100 for the maximum and minimum sized wave vectors of its Fermi surface.

z Trigonal (3)

x Binary (1)

y Bisectrix (2)

0886-F04-05.2

Bismuth-Antimony (BiSb)

Figure 2. Band structure of Bi

1-x

alloy as a function of Sb concentration x [7]. The Brillouin

zone is shown as an inset, indicating the location of one of the L points, one of the T points, and

3 of the 6 H points.

Bismuth and Antimony are both group V elements and semimetals in bulk form. They are

completely miscible with each other, are isoelectronic, and have very similar chemical

properties. However, due to the larger structural distortions in Sb, the valence band of Sb is

located at the H points instead of the T points (see Figure 2). The introduction of Sb into Bi

changes the band structure of Bi and gives rise to a transition between a semimetal and a

semiconductor (see Figure 2). The extra control on the system parameters by the addition of Sb

provides a promising approach to achieve a desirable band structure for the desired

thermoelectric applications.

RESULTS

Bi thin film calculation

To understand the behavior of the Bi

1-x

system under investigation, the Schrödinger

equation for this system needs to be solved for the energy eigenvalues and wavefunctions.

However, from the effective mass theorem [8], knowing the envelope wave function is sufficient

to describe many properties of the system. Thus, it is sufficient within the effective mass

approximation to solve for the envelope function of the system without solving for the exact

wavefunctions.

For each electronic energy band (conduction or valence), we start with the effective mass

model

(,,) (,,)

yz E xyz

αψ ψ

−∇••∇ =

(1)

where the inverse effective mass tensor is given by

Bismuth Antimony

0886-F04-05.3

11 12 13

12 22 23

13 23 33

ααα

αααα

ααα

−

⎛⎞

⎜⎟

≡=

⎜⎟

⎝⎠

(2)

and when we carry out the dot products in Equation (1) , we obtain the result

222 2 2 2

11 22 33 12 13 23

222 2

222

xyz xyxzyz

ψψψ ψ ψ ψ

αα α α α ψ

∂∂∂ ∂ ∂ ∂

+++ + + =−

∂∂∂ ∂∂∂∂∂∂=

(3)

If we let the trigonal axis be the film growth direction, the envelope function could then be

written as

(,,) () [ ]

ik y

ik x

ik z

xyz uze e e

= ,

(4)

and the equation can be solved for the wavefunctions and the eigenenergies to obtain:

22 2

13 23 13 23

11 22 12

33 33 33

{( ) ( ) (2 )}

22 2

xy xy

Ek k kku

αα αα

αα α

+−+ +−+ +− +

∂

=−

∂

== =

(5)

Once the eigenenergies and wavefunctions for each subband for the film are obtained by solving

Equation (5), the properties of the thin film system can be studied. We are interested in both the

solutions for general k vectors and for the solution at the bandedge. We note that in the case of a

thin film solution for the band edge energy (k

=0), this solution is very similar to the particle-

in-a-box solution. Putting the eigenvalue solution for the band edge energy in the form of

particle-in-a-box solution results in an equation of the following form for each subband

222

()

Ek k

(6)

where

= is Planck’s constant, L = film thickness,

* = inverse effective mass in the film growth

direction for the band under investigation, and n=1,2,3,… is the subband index. For our case

where the film growth direction is along the trigonal axis, the inverse effective mass is

Applying Equation (6) to the Bi thin film system with the growth direction along the trigonal

axis for each subband at a temperature range of around 77K, it is found that the semimetal-

semiconductor transition occurs at a critical film thickness (d

) of about 65nm (see Figure 3).

Previous publications have estimated a d

of 100nm [9] and 13nm [10] for the same system

under investigation. This discrepancy is mainly due to the different temperature range in interest

and the lack of consideration for the anisotropic nature of Bi from previous works.

Fermi level and transport properties are other parameters of interest for our system. Due to

the non-parabolic nature of the L conduction bands and the different transport effective masses

between the L electrons and the H or T holes, the Fermi level will change depending on the film

thickness and Sb concentration. The Fermi level calculation will be presented in detail along

with the transport properties evaluation in our upcoming publication.

0886-F04-05.4

Figure 3. Bi thin film calculation of the energy for the valence and conduction band extrema as

a function of film thickness for the film growth direction along the trigonal axis. The

semimetallic-semiconducting transition occurs at a film thickness of around 65nm.

BiSb thin film calculation

Combining the thin film calculation (from the previous subsection) with the band structure

of the BiSb alloy (see Figure 2), a BiSb 2D film phase diagram is generated (see Figure 4).

The BiSb 2D film phase diagram possesses similar physics when compared with the

previous work for the nanowire system [1]. Starting from the pure Bi region, the increase in Sb

concentration decreases the overlap between the T points and L points, resulting in an increase in

film thickness (a decrease in the amount of quantum confinement) needed for the occurrence of

the semimetal-semiconductor transition. A similar behavior is observed when we start from the

Sb-rich regions. Two especially interesting phenomenon for the phase diagram worth noting are

that: (1) the system is gapless at each of the semimetal-semiconductor transition boundaries and

(2) the valence band T points, valence band H points, and conduction and valence bands L points

of the Bi thin film system all have the same energy at the middle point of the phase diagram.

Thus, at regions near the point of high band degeneracy, this system not only has the potential of

being a good candidate for low temperature thermoelectric applications, it may also be used as an

extremely sensitive meV detector due to its high density of states (DOS) near its band extrema.

Due to the anisotropic nature of Bi and the different confinement direction between this

work (the trigonal direction) and previous work (the bisectrix and binary directions) [1], there is

no clear direct comparison between these works of the length scales for the semimetal-

semiconductor transition. However, in general, for an isotropic or a close-to-isotropic system,

the length scales for the observation of quantum effects should increases as the dimension of

confinement increases. In the case of thin films, quantum confinement is in the film direction,

while for the nanowires, quantum confinement occurs in the two directions normal to the axis of

the quantum wire.

Decreasing film thickness

Semimetal

Semiconductor

0886-F04-05.5

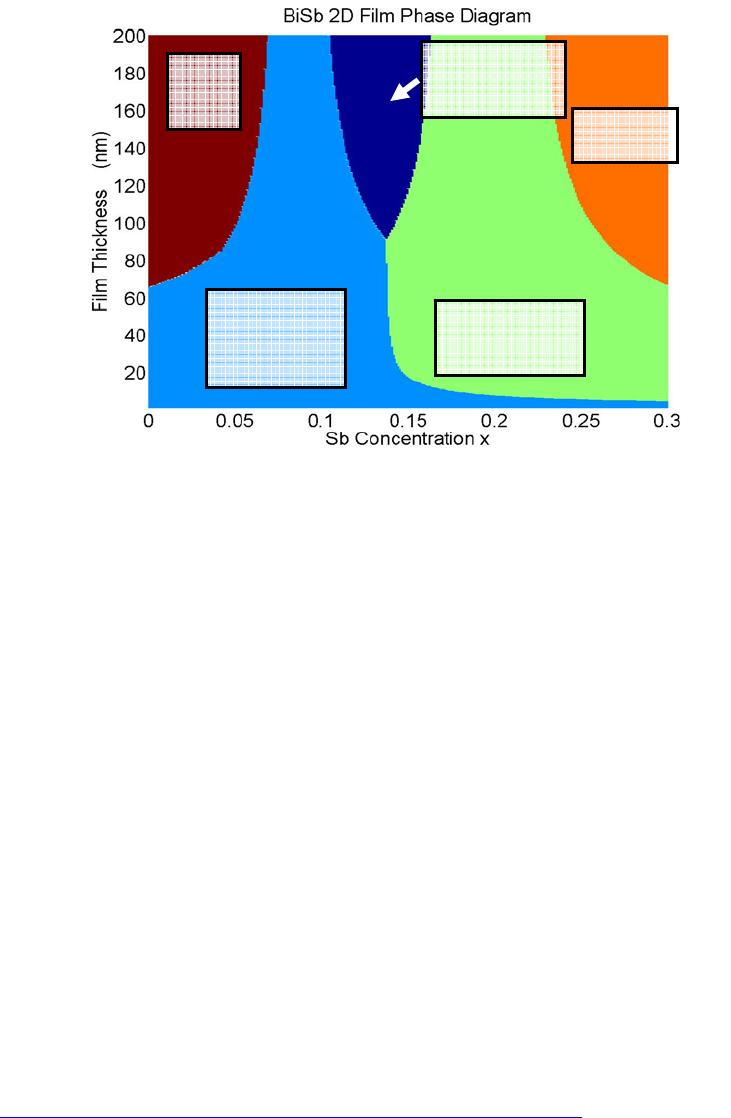
Figure 4. A BiSb 2D film Phase Diagram. The semimetallic and semiconducting regions are

noted. For each region, the location of the valence band extrema and the conduction band

extrema are indicated by the notation valence

öconduction. And for the semiconducting

phases, the indirect and direct gap phases are distinguished.

SUMMARY

Using the quantum confinement principle and the addition of Sb, a 2D Phase Diagram for

BiSb film has been computed. This 2D Phase Diagram gives guidelines for designing desired

BiSb thin films for thermoelectric applications.

ACKNOWLEDGEMENTS

The authors gratefully thank valuable discussions with Dr. Gene Dresselhaus, Dr. Oded

Rabin, and Dr. Yu-Ming Lin, and support from NSF/NIRT (CTS-0506830) for this work.

REFERENCES

1. O. Rabin, Y.-M. Lin, and M.S. Dresselhaus, Appli. Phys. Lett., 2001.

79(1): p. 81-83.

2. L.D. Hicks and M.S. Dresselhaus, Phys. Rev. B, 1993.

47: p. 12727-12731.

3. L.D. Hicks and M.S. Dresselhaus, Phys. Rev. B, 1993.

47: p. 16631-16634.

4. G. Chen, Phys. Rev. B, 1998.

57: p. 14958-14973.

5. R. Venkatasubramanian, et al., Nature, 2001.

413: p. 597-602.

6. http://www.pmel.org/HandBook/PeriodicTable/periodic.htm

7. B. Lenoir, et al., J. Phys. Chem. Solids, 1998.

59(1): p. 129-134.

8. T.P. Orlando, S.D. Senturia, and P.L. Hagelstein, Physics for Solid State Applications. p.

Chapter 7.

9. V.N. Lutskii, Sov. Phys. - JETP. Lett., 1965.

2: p. 245-248.

10. S. Takaoka and K. Murase, J. Phys. Soc. Jpn., 1985.

54(6): p. 2250-2256.

direct

semiconductor

L->L

indirect

semiconducto

T->L

indirect

semiconductor

H->L

semimetal

L->H

semi-

metal

L->T

0886-F04-05.6