R3.5.1

A Novel Approach for True Work Function Determination of Electron-Emissive Materials

by Combined Kelvin Probe and Photoelectric Effect Measurements

Bert Lägel, Iain D. Baikie, Konrad Dirscherl and Uwe Petermann,

Department of Applied Physics, The Robert Gordon University, Aberdeen, UK.

ABSTRACT

For the development of new electron-emissive materials knowledge of the work function (φ)

and changes in φ is of particular interest. Among the various methods, the ultra-high vacuum

(UHV) compatible scanning Kelvin Probe has been proven to be a superior technique to measure

work function changes due to e.g. UHV cleaning processes, chemical contamination, thermal

processing etc. with high accuracy (<1meV).

The Kelvin Probe measures local work function differences between a conducting sample and

a reference tip in a non-contact, truly non-invasive way over a wide temperature range. However,

it is an inherently relative technique and does not provide an absolute work function if the work

function of the tip (φ

tip

) is unknown.

Here, we present a novel approach to measure φ

tip

with the Kelvin Probe via the photoelectric

effect, where a Gd foil is used as the photoelectron source. This method thus provides the true

work function of the sample surface with an accuracy of approx. 50meV. We demonstrate the

application of the technique by in situ work function measurements on evaporated layers of the

low work function material LaB

on a Re substrate and follow the changes in φ of LaB

due to

the surface adsorption of residual gas molecules. Thus, the extended Kelvin Probe method

provides an excellent tool to characterise and monitor the stability of low work function surfaces.

INTRODUCTION

The work function is an extremely sensitive indicator of changes in surface and interface

chemical composition, adsorbate induced surface dipole and surface roughness. Further, for the

characterisation of electron emissive materials, the work function is one of the most important

parameters and low φ materials are of particular interest. However, due to the adsorption of

residual gases, the work function of these materials is known to increase with time, adversely

affecting their emission properties.

The Kelvin Probe [1, 2] can be used to monitor these work function changes in a non-contact,

non-invasive way with high accuracy (< 1meV) [3, 4] up to temperatures of approx. 900K. It has

been utilised e.g. for thin film studies [5, 6, 7], characterisation of oxides and thin films [8],

semiconductor surface processing [9] and surface charge imaging [10], investigation of the

adsorption kinetics of oxygen on Si(111) surfaces [11] as well as for biological applications [12].

However, the Kelvin Probe is an inherently relative technique as it measures the average

work function or contact potential difference (CPD) between a vibrating reference electrode (the

tip) and the surface under investigation. Thus, in order to obtain the absolute value of the work

function of the specimen, it is necessary to know the work function of the reference electrode,

tip

. This could be determined e.g. by a CPD measurement on a clean reference surface. The

accuracy of this method however depends on tabulated φ values, which are often valid only for

the given experimental setup and the assumption of a clean reference surface.

R3.5.2

We have developed a relatively simple extension of the technique as an approach for a more

reliable method to determine φ

tip

. This is achieved via measurement of the current voltage (I-V)

characteristic of the photoelectric emission from a low work function surface, such as Gd,

illuminated by monochromatic light of a fixed wavelength as discussed e.g. in [13]. The work

function of any conductor or semiconductor can then be obtained by subsequent Kelvin Probe

CPD measurements.

We have utilised this technique to investigate low work function materials as possible targets

for use in Hyperthermal Surface Ionisation (HSI), a new mass spectroscopy ionisation technique

which offers high ionisation efficiency and low amounts of cracking products [14, 15].

Lanthanum Hexaboride (LaB

) is particularly interesting in this respect because of its low work

function and its surface re-activation capabilities after adsorption of residual gases via flash-

annealing [16].

EXPERIMENTAL METHOD

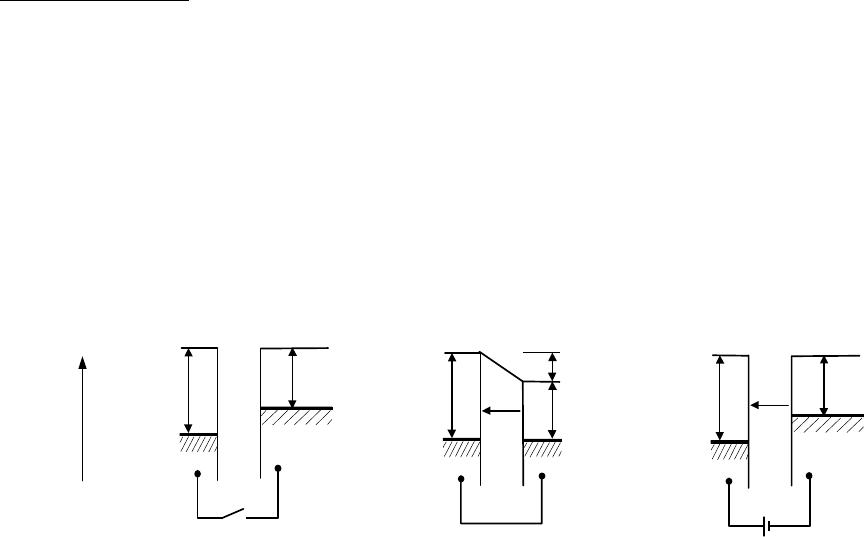
The Kelvin Method

The Kelvin Probe consists of a flat circular electrode (reference electrode, tip) suspended

above and parallel to a stationary electrode (the specimen, S), thus creating a simple capacitor. If

an external electrical contact is made between the two electrodes their Fermi levels equalise and

the resulting flow of electrons from the metal with the lower work function produces a contact

potential difference, V

CPD

, between the plates as shown in fig. 1(b):

CPD

= φ

− φ

tip

, (1)

where e is the electronic charge and φ

tip

and φ

are the work functions of the tip and sample,

respectively. By vibrating the probe, a varying capacitance is produced which causes a current to

flow back and forth between the plates.

≠

− +

Electronic Energy

(a)

Vac

tip

= -V

CPD

(c)

tip

CPD

(b)

tip

Figure 1. Electron energy level diagrams of two different metals (a) without contact, (b) with

external electrical contact, where E indicates the electrical field between the plates, and (c) with

inclusion of the backing potential.

tip

and

refer to the Fermi levels of the tip and sample,

respectively.

Inclusion of a variable “backing potential” V

in the external circuit permits biasing of one

electrode with respect to the other: at a unique point, where

CPDb

VV −= , the electrical field

between the plate vanishes, see fig. 1(c), resulting in a null output signal. The work function

difference between the electrodes is thus equal and opposite to the DC potential necessary to

produce a zero output signal.

R3.5.3

The CPD measurements were performed with a UHV compatible Kelvin Probe that

incorporates advanced “off-null” detection, where the balance point is determined by linear

extrapolation rather than nulling with a resolution of <1mV as well as automatic control of the

tip-to-sample spacing, which is an important requirement for accurate measurements [4, 17].

Measurements can be performed with a frequency of up to 1 data point per second.

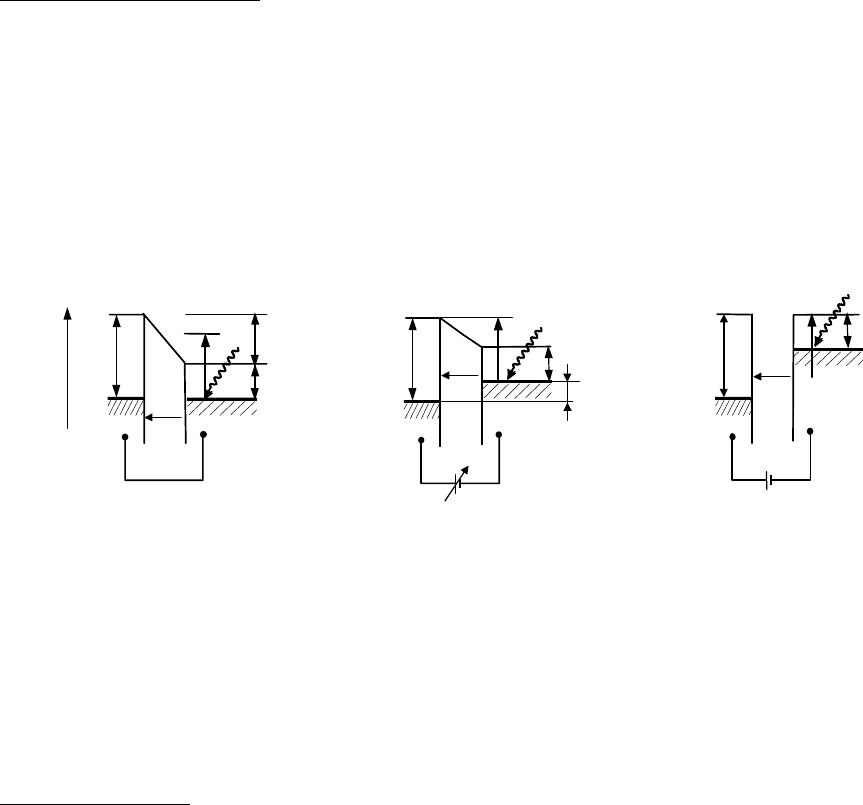
Photocurrent Measurement

In the photoelectric measurement mode the capacity of the arrangement is kept constant. The

photoelectrons emitted from a low work function surface (S) illuminated by monochromatic light

of energy E

= hν with φ

tip

> hν > φ

are collected by the Kelvin Probe tip and measured as a

function of the applied backing potential V

(see figure 2). It can be seen that, at the onset of the

photocurrent collected at the Kelvin Probe tip, (fig. 2b), the work function of the tip equals the

photon energy E

plus a required bias potential supplied by V

, i.e.,

btip

Vh +=

νφ

(onset). (2)

≠

Electronic Energy

(a)

CPD

tip

Vac

tip

= V

(onset)

(b)

tip

= -V

CPD

(c)

Figure 2. Energy level diagrams of the Kelvin Probe in photocurrent measurement mode with

tip

: (a) no photoelectrons are collected at the tip, (b), the onset of the photocurrent is

measured where

tip

= h

+ V

(onset) and in (c) the saturation current where

CPDb

VV −= .

With increasing bias potential, analogous to the Fowler theory of photoemisson from metals

near threshold [18], the photocurrent increases with the square of V

: I

∝ V

. When V

equals

-V

CPD

(fig. 2c), electrons emitted from energy states below the Fermi level with virtually zero

velocity are only just able to reach the collector and the photocurrent will saturate.

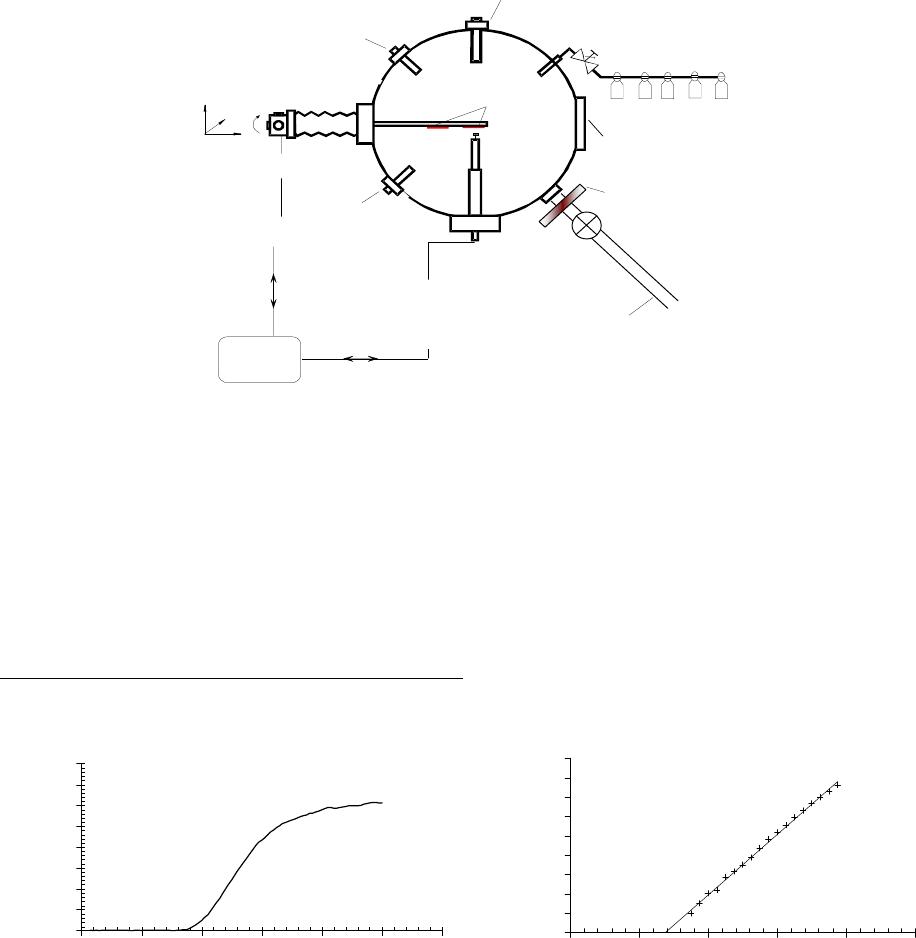
Experimental Setup

The experiments were carried out in a UHV chamber as shown in fig. 3 with a base pressure

of <4×10

-9

Torr. A polycrystalline gadolinium foil (25×12×0.1mm

) was used as the

photoelectron source. The sample was cleaned by repeated resistive heating up to 1200K for

several minutes. Gd has the advantage of having a relatively low work function of 3.1eV [19] and

is available in form of thin foils. Further, we found that the work function of Gd remained stable

within 100meV over several days. For photoemisson measurements the Gd foil was illuminated

by a 100W Hg-Cd-Zn spectral lamp through a sapphire viewport which is transparent for

wavelengths down to 200nm. The 312.6nm Hg emission was selected by a narrowband

interference filter (FWHM = ± 20nm).

R3.5.4

LaB

(purity 99%) films were generated via evaporation onto a polycrystalline rhenium foil

(25×12×0.025mm

, purity 99.99%). The foil was cleaned by repeated flash annealing to

temperatures above 2000K. The work functions of the samples were determined by first

obtaining φ

tip

of the Kelvin Probe via the photoeffect I-V measurement and a subsequent Kelvin

Probe CPD measurement of the respective sample. The UHV system was darkened during the

measurements and all filaments were extinguished.

Host

Computer

KP / SKP PE

Probe Oscillator

Pre-Amplifier

AD Converter

DA converter

I-V Converter

Pre-Amplifier

X-Y-Z Translation Stage

Fast Entry

Load Lock

Gas Inlet

System

Kelvin Probe

Samples

Stepper Motor

Control Unit

Ar O

Quadrupole Mass

Analyser

Ion Gauge

Pulsed Nozzle Valve

Optical Rail

Bandpass Filter

(312.6nm)

Hg, Zn, Cd

Spectral Lamp

e-Beam Evaporator

Figure 3. Schematic of the UHV system with its associated peripherals and facilities

For CPD/photocurrent measurements the signal collected from the stainless steel tip

(Ø2.5mm) is converted into a voltage signal by a high gain (10

), low noise operational amplifier,

filtered and digitised by the AD-converter for further signal processing by the host PC. The

computer program controls tip oscillation and backing potential. This design thus provides a fully

automated measurement system.

RESULTS AND DISCUSSION

Kelvin Probe Tip Work Function Determination

Figure 4 shows typical data of the photoelectron emission from the Gd surface.

Figure 4. Typical photoemission data used to determine the work function of the Kelvin Probe:

(a) the current-voltage (I-V) curve and (b) the plot I

1/2

versus bias voltage. Note that only data

from the linear portion of the curves are included in the fit.

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0 0.4 0.8 1.2 1.6 2

/ V

1/2

/ a.u.

0.2

0.4

0.6

0.8

1.2

1.4

1.6

-1012345

/ V

/ nA

(a) (b)

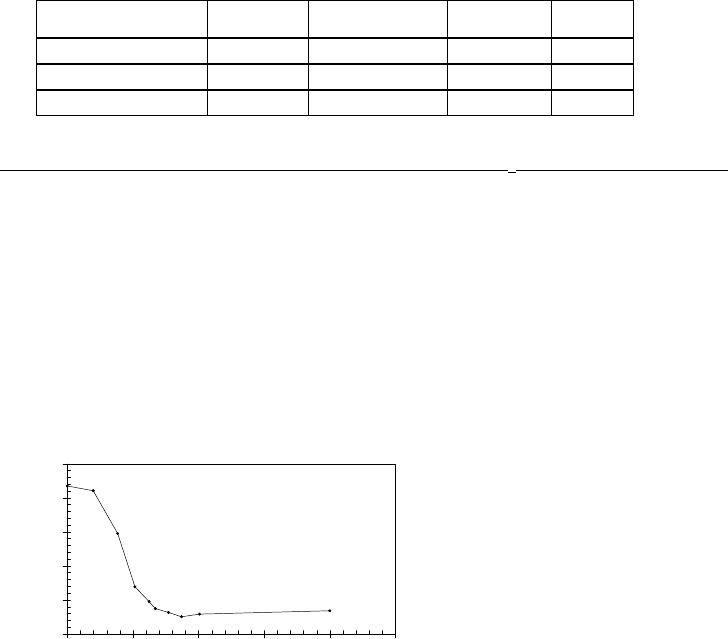
R3.5.5

In order to determine the onset of the photocurrent I

, the square root of I

is plotted versus

the applied bias voltage V

(fig 4b) and a least square fit of the linear part of the curve is

extrapolated to zero current. φ

tip

and φ

Sample

are then calculated via equations 1 and 2,

respectively. The results of the measurements are summarised in table I. The uncertainty of the

extrapolation is approx. ± 20mV. Further, taking the measurement error due to the thermal

energy distribution into account (26mV at 300K) and small changes in tip work function during

the measurement (<20meV), we estimate the overall error of the work function measurement to

be ± 50meV.

The work function determined for Gd (3.075 ± 0.050)eV

is, within the measurement error, in

agreement with that of (3.1 ± 0.150)eV

given in [19]. The work function measured for the clean

Re substrate was used as a calibration point for the absolute work function scale in fig. 5.

Table I. Results of the measurements to determine tip and sample work functions.

Measurement E

/ eV V

(onset) / V V

CPD

/ V

φφ

φ / eV

Kelvin Probe tip 3.966 0.551± 0.016

4.518

-1.443 3.075

0.653 5.171

Application to Work Function Measurements of LaB

on Polycrystalline Re

In order to characterise the LaB

evaporation process, the work function change of the

Re/LaB

system was measured at different stages of the evaporation as shown in figure 5. After

an initial rapid decrease the work function changes only in small steps with further evaporation,

gradually achieving approx. 3.3eV. However, if the surface is ‘activated’ by flashing it to

1500°C, a further work function decrease to 2.536eV is obtained. The necessity for such an

activation procedure might be caused either by contamination or, indeed, a rearrangement of the

LaB

structure since its work function is known to depend strongly on the surface stoichiometry

of the compound [20].

The work function increase due to the adsorption of residual gas molecules of the LaB

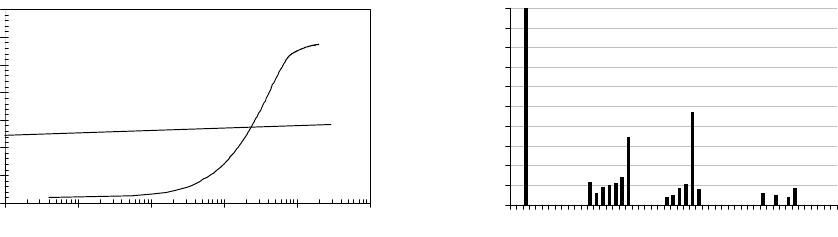
surface after activation and, for comparison, Gd, is shown in figure 6. With respect to the LaB

surface, we clearly observe 2 adsorption stages. The first one, marked AB, with an almost

constant gradient above 10L and the second one, after approx. 80L, with a lower and rather

continuous gradient leading to a work function of 3.65eV after an exposure of 200L.

Figure 5. Work function change

during evaporation of LaB

onto a

Re foil held at 300K. The current

onto the sample due to the partly

ionised molecular beam was used as

a measure of the particle flux.

3.5

4.5

5.5

0 5 10 15 20 25

particle flux / a.u.

φ(

φ(φ(

φ(

Re/LaB

)

R3.5.6

This shows that LaB

is rather easily poisoned at 300K by the adsorption of the residual gas,

the largest component of which is molecular hydrogen. In contrast, although having a higher

initial work function, φ(Gd) increases by only 70meV after 200L exposure.

Figure 6. (a) Work function increase of LaB

and Gd due to the adsorption of residual gas

molecules at 300K. (b) The relative composition of the residual gas envelope at a base pressure

of 3.7

-9

Torr.

CONCLUSIONS

We have demonstrated the feasibility of a novel approach to determine the work function of

the reference tip of a Kelvin Probe via photoelectric current measurements on Gd using a

minimum of additional instrumentation. We found that the work function of Gd remains stable

over a prolonged period of time in the upper UHV pressure region of approx. 4×10

-9

Torr and is

therefore best suited for this purpose. The measurement error is estimated to be ± 50meV.

Using the new technique we have followed the evaporation of LaB

onto a polycrystalline Re

substrate. After activation, the surface work function at 300K was (2.536 ± 0.050) eV, increasing

to (3.65 ± 0.050) eV after an exposure of 200L to the residual gas. This indicates a very high

sensitivity of the work function of LaB

to the adsorption of gas molecules which may restrict its

use for applications requiring a stable low work functions surface at low temperatures.

ACKNOWLEDGEMENTS

This work was supported by EPSRC and DERA.

REFERENCES

1. Lord Kelvin, Philos. Mag

, 82 (1898)

2. W.A. Zisman.

Rev. Sci. Instrum.

, 367 (1932)

3. I.D. Baikie, K.O. Vanderwerf, H. Oerbekke, J. Broeze, A. Vansilfhout, Rev. Sci. Instrum.

930 (1989)

I.D. Baikie, P.J. Estrup, Rev. Sci. Instrum.

, 3902 (1998)

5. M. Schmidt, H. Wolter, M. Nohlen, K.Wandelt, J. Vac. Sci Technol.

A12

, 1818 (1994)

6. E. Kopatzki, H.G. Keck, I.D Baikie, J.A. Meyer, ,R.J. Behm, Surf. Sci.

345

, L11 (1996)

7. I.D. Baikie, U. Petermann, B. Lägel, Surf. Sci.

433-435

, 770 (1999)

100

0 3 6 9 12 15 18 21 24 27 30 33 36 39 42 45 48

mass / a.m.u.

relative composition / %

2.5

2.7

2.9

3.1

3.3

3.5

3.7

3.9

0.01 0.1 1 10 100 1000

Exposure / Langmuir

φφ

(Re/LaB

) / eV

LaB

(a) (b)

R3.5.7

I.D. Baikie, G.H Bruggink in Materials Reliability in Microelectronics III, edited by K.P. Rodbell,

W.F. Filter, H.J. Frost, P.S. Po,

(Mater. Res. Soc. Proc.

309

, Pittsburgh, PA, 1993), pp. 35-40

I.D. Baikie in Chemical Perspectives of Microelectronic Materials II, edited by L.V. Interrante, K.F.

Jensen, L.H. Dubois, M.E. Gross

(Mater. Res. Soc. Proc.

204

, Pittsburgh, PA, 1991), pp. 363-368

10. B. Lägel , I.D. Baikie, U. Petermann in Defect and Impurity Engineered Semiconductors and

Devices II, edited by S. Ashok, J. Chevallier, K. Sumino, B.L. Sopori, W. Goetz, (Mater. Res.

Soc. Proc.

510

, Pittsburgh, PA, 1998), pp. 619-625

11. U. Petermann, I.D. Baikie, B. Lägel, Thin Solid Films

343-344

, 492 (1999)

12.

I.D. Baikie, P.J.S. Smith, D.M. Porterfield, P.J. Estrup, Rev. Sci. Instrum.

, 1842 (1999)

13. L. Apker, E. Taft, J. Dickey, Phys. Rev.

, 46 (1947)

14. A. Danon, A. Amirav, Isr. J. Chem.

, 443 (1989)

15. A. Danon, A. Amirav, Int. J. Mass Spectrom. Ion. Processes

, 139 (1990)

16. J.M. Lafferty, J. Appl. Phys.

, 299 (1951)

17.

I.D. Baikie, S. Mackenzie, P.J.Z. Estrup and J.A. Meyer, Rev. Sci. Instrum.

, 1326 (1991)

18. R.H. Fowler, Phys. Rev.

, 45 (1931)

19. D.E. Eastman, Phys Rev.

, 1 (1970)

20. E.K. Storms, B.A. Mueller, J. Appl. Phys.

, 3691 (1979)