
Fast 6D Pose Estimation from a Monocular
Image Using Hierarchical Pose Trees
Yoshinori Konishi
1(
B
)
, Yuki Hanzawa
1
, Masato Kawade
1
,
and Manabu Hashimoto
2
1
OMRON Corporation, Kyoto, Japan
{ykoni,hanzawa,kawade}@ari.ncl.omron.co.jp
2
Chukyo University, Nagoya, Japan
Abstract. It has been shown that the template based approaches could
quickly estimate 6D pose of texture-less objects from a monocular image.
However, they tend to be slow when the number of templates amounts
to tens of thousands for handling a wider range of 3D object pose. To
alleviate this problem, we propose a novel image feature and a tree-
structured model. Our proposed perspectively cumulated orientation fea-
ture (PCOF) is based on the orientation histograms extracted from ran-
domly generated 2D projection images using 3D CAD data, and the
template using PCOF explicitly handle a certain range of 3D object
pose. The hierarchical pose trees (HPT) is built by clustering 3D object
pose and reducing the resolutions of templates, and HPT accelerates 6D
pose estimation based on a coarse-to-fine strategy with an image pyra-
mid. In the experimental evaluation on our texture-less object dataset,
the combination of PCOF and HPT showed higher accuracy and faster
speed in comparison with state-of-the-art techniques.
Keywords: 6D pose estimation
· Texture-less objects · Template
matching
1 Introduction
Fast and accurate 6D pose estimation of object instances is one of the most
important computer vision technologies for various robotic applications both
for industrial and consumer robots. In recent years, low-cost 3D sensors such as
Microsoft Kinect became popular and they have often been used for object detec-
tion and recognition in academic research. However, much more reliability and
durability are required for sensors in industrial applications than in consumer
applications. Thus the 3D sensors for industry are often far more expensive,
Electronic supplementary material The online version of this chapter (doi:10.
1007/978-3-319-46448-0
24) contains supplementary material, which is available to
authorized users.
c
Springer International Publishing AG 2016
B. Leibe et al. (Eds.): ECCV 2016, Part I, LNCS 9905, pp. 398–413, 2016.
DOI: 10.1007/978-3-319-46448-0
24

Fast 6D Pose Estimation Using Hierarchical Pose Trees 399
Fig. 1. Our new template based algorithm can estimate 6D pose of texture-less and
shiny objects from a monocular image which contains cluttered backgrounds and partial
occlusions. It takes an average of approximately 150 ms on a single CPU core.
larger in size and heavier than the consumer ones. Additionaly, most of 3D sen-
sors even for industry cannot handle objects with specular surfaces, are sensitive
to illumination conditions and require cumbersome 3D calibrations. For those
reasons, monocular cameras are mainly used in the current industrial applica-
tions, and fast and accurate 6D pose estimation from a monocular image is still
an important technique.
Many of industrial parts and products have little texture on their surfaces,
and they are so-called texture-less objects. Object detection methods based on
keypoints and local descriptors such as SIFT [1] and SURF [2] cannot handle
texture-less objects because they require rich textures on the regions of tar-
get objects. It has been shown that template based approaches [3–9] which use
whole 2D projection images from various viewpoints as their model templates
successfully dealt with texture-less objects. However, they suffer from the speed
degradation when the numbers of templates are increased for covering a wider
range of 3D object pose.
We propose a novel image feature and a tree-structured model for fast tem-
plate based 6D pose estimation (Fig. 1). Our main contributions are as follows:
• We introduce perspectively cumulated orientation feature (PCOF) extracted
using 3D CAD data of target objects. PCOF is robust to the appearance
changes caused by the changes in 3D object pose, and the number of templates
are greatly reduced without loss of pose estimation accuracy.
• Hierarchical pose trees (HPT) is also introduced for efficient 6D pose search.
HPT consists of hierarchically clustered templates whose resolutions are dif-
ferent at each level, and it accelerates the subwindow search by a coarse-to-fine
strategy with an image pyramid.
• We make available a dataset of nine texture-less objects (some of them have
specular surfaces) with the ground truth of 6D object pose. The dataset
includes approximately 500 images per object taken from various viewpoints,
and contains cluttered backgrounds and partial occlusions. 3D CAD data for
training are also included.
1
1
http://isl.sist.chukyo-u.ac.jp/Archives/archives.html.
400 Y. Konishi et al.
The remaining contents of the paper are organized as follows: Sect. 2 pre-
sented related work on 6D pose estimation, image features for texture-less objects
and search data structures. Section 3 introduces our proposed PCOF, HPT and
6D pose estimation algorithm based on them. Section 4 evaluates the proposed
method and compare it with state-of-the-art methods. Section 5 concludes the
paper.
2 Related Work
6D Pose Estimation. 6D pose estimation has been extensively studied since
1980s and in the early days the template based approaches using a monocular
image [3–5] were the mainstream. Since the early 2000s, keypoint detections
and descriptor matchings became popular for detection and pose estimation
of 2D/3D objects due to their scalability to the increasing search space and
robustness to the changes in object pose. Though they can handle texture-less
objects when using line features as the descriptors for matching [10,11], they
were fragile to cluttered backgrounds because the line features were too simple
to suffer from many false correspondences in the backgrounds.
Voting based approaches as well as template based approaches have a long
history, and they have also been applied to detection and pose estimation of
2D/3D objects. Various voting based approaches were proposed for 6D pose
estimation such as voting by dense point pair features [12], random ferns [13],
Hough forests [14], and coordinate regressions [15]. Though they are scalable to
increasing image resolutions and the number of object classes, the dimensionaliy
of search space is too high to estimate precise object pose (excessive quantiza-
tions of 3D pose space are required). Thus they need post-processings for pose
refinements, which spend additional time.
CNN based approaches [16–18] recently showed impressive results on 6D
pose estimations. However, they take a few seconds even when using GPU and
they are not suitable for robotic applications where near real-time processing is
required on poor computational resources.
Template based approaches have been shown to be practical both in accuracy
and speed for 6D pose estimation of texture-less objects [6,7,19]. Hinterstoisser
et al. [8,9] showed their LINE-2D/LINE-MOD which is based on the quantized
orientations and the optimally arranged memory quickly estimated 6D pose of
texture-less objects against cluttered backgrounds. LINE-2D/LINE-MOD was
further improved by discriminative training [20] and by hashing [21,22]. However,
the discriminative trainig required additional negative samples and the hashing
led to suboptimal performance in the estimation accuracy.
Image Features for Handling Texture-less Objects. Image features used
in template matching heavily influence the performance of pose estimation from
a monocular image. Though edges based template matchings have been applied
to detection and pose estimation of texture-less objects, they often required the
additional algorithm such as segmentation [19] or the additional hardware like
a multi-flash camera [6] to suppress cluttered edges in the backgrounds.
Fast 6D Pose Estimation Using Hierarchical Pose Trees 401
It has been shown that the gradient direction vectors [23] and the quantized
gradient orientations [24] were robust to cluttered backgrounds and illumination
changes. However, it was pointed out that the similarity scores based on these
features rapidly declined even if only slight changes in object pose occurred. To
overcome this problem, dominant orientations within a grid of pixels (DOT) [25]
and spread orientation which allowed some shifting in matching [8] were pro-
posed. DOT and spread orientation are robust to the pose changes and slight
deformations of target objects. However, they relax matching conditions both in
foregrounds and backgrounds, and this possibly degrade the robustness to clut-
tered backgrounds. Konishi et al. [26] introduced cumulative orientation feature
(COF) which was robust to the apperance changes caused by the changes in 2D
object pose. However, COF did not explicitly handle appearance changes caused
by the changes in 3D object pose.
Tree-Structured Models for Efficient Search. Search strategies and data
structures are also important for template based approaches. The tree-structured
models are popular in the nearest neighbor search for image classification
[27–29] and for joint object class and pose recognition [30]. These tree-structured
models were also used in joint 2D detection and 2D pose recognition [31]and
joint 2D detection and 3D pose estimation [32]. Though they offered efficient
search in 2D/3D object pose space but not in 2D image space (x-y translations).
The well-known efficient search in 2D image space is the coarse-to-fine search
[33]. Ulrich et al. [7] proposed the hierarchical model which combined the coarse-
to-fine search and the viewpoint clustering based on similarity scores between
templates. However, their model is not fully optimized for the search in 3D pose
space when 2D projection images from separate viewpoints are similar, as is
often the case with texture-less objects.
3 Proposed Method
Our proposed method consists of a image feature for dealing with the appearance
changes caused by the changes in 3D object pose (Sect. 3.1) and a hierarchical
model for the efficient search (Sect. 3.2). The template based 6D pose estimation
algorithm using both PCOF and HPT is described in Sect. 3.3.
3.1 PCOF: Perspectively Cumulated Orientation Feature
In this subsection, the way how to extract PCOF is explained using L-Holder
showninFig.2(a) which is a typical texture-less object. Our PCOF is developed
from COF [26] and the main difference is two-fold: One is that PCOF explicitly
handle appearance changes caused by the changes in 3D object pose, whereas
COF can handle appearance changes only by 2D pose changes. Another is that
PCOF is based on a probabilistic representation of quantized orientations at
each pixel, whereas COF uses all the orientations observed at each pixel.

402 Y. Konishi et al.
(a)
(b)
Fig. 2. (a) 3D CAD data of L-Holder, its coordinate axes and a sphere for viewpoint
sampling. (b) Examples of the generated projection images from randomized viewpoints
around the viewpoint on z-axis (upper-left image). Surfaces of objects are drawn by
randomly selected colors in order to extract distinct image gradients.
Firstly many 2D projection images are generated using 3D CAD data from
randomized viewpoints (Fig. 2(a)). The viewpoints are determined by four para-
meters those are rotation angles around x-y axes, a distance from the center of
the object and a rotation angle around a optical axis. The range of randomized
parameters should be limited so as to a single template can handle the appear-
ance changes caused by the randomized parameters. In our research, the range
of randomization were experimentally determined and those were ±12
◦
around
x-y axes, ±40 mm in the distance and ±7.5
◦
around the optical axis. Figure 2(b)
shows examples of generated projection images. The upper-left image of Fig. 2(b)
is the projection image from the viewpoint where all rotation angles are zero and
the distance from the object is 680 mm, and this viewpoint is at the center of
these randomized examples. In generation of projection images, the neighboring
meshes where the angle between them is larger than a threshold value are drawn
by different color in order to extract distinct image gradients. In this study the
threshold was 30
◦
.
Secondly image gradients of all the generated images are computed using
Sobel operators (the maximum gradients among RGB channels are used). We
use only the gradient directions discarding gradient magnitudes because the
magnitudes depend on the randomly selected mesh colors. The colored gradient
directions of the central image (the upper-left in Fig. 2(b)) are shown in Fig. 3(a).
Then the gradient direction is quantized into eight orientations disregarding its
polarities (Fig. 3(b)), and the quantized orientation is used for voting to the
orientation histogram at each pixel. The quantized orientations of all the gener-
ated images are voted to the orientation histograms at the corresponding pixels.
Lastly the dominant orientations at each pixel are extracted by thresholding
the histograms and they are represented by 8-bit binary strings [25]. The maxi-
mum frequencies of the histograms are used as weights in calculating a similarity
score.

Fast 6D Pose Estimation Using Hierarchical Pose Trees 403
(a)
(b)
(c)
Fig. 3. (a) Colored gradient directions of the upper-left image in Fig. 2(b). (b) Quanti-
zation of gradient directions disregarding their polarities. (c) Examples of the orienta-
tion histograms, binary features (ori) and their weights (w) on arbitrarily selected four
pixels. Red dotted lines show the threshold for feature extraction. (Color figure online)
The template T with n PCOF represented as follows:
T : {x
i
,y
i
,ori
i
,w
i
|i =1, ..., n} , (1)
and the similarity score is given by following equation,
score(x, y)=
n
i=1
δ
k
(ori
I
(x+x
i
,y + y
i
)
∈ ori
T
i
)
n
i=1
w
i
. (2)
If the quantized orientation of the test image (ori
I
) is included in the PCOF
template (ori
T
), the weight (w) is added to the score. The delta function in
Eq. (2) is calculated quickly by a bitwise AND operation (the symbol ∧). Addi-
tionally, this calculation can be accelerated using SIMD instructions where mul-
tiple binary features are matched by a single instruction.
δ
i
(ori
I
∈ ori
T
)=
w
i
if ori
I
∧ ori
T
> 0,
0 otherwise.
(3)
The orientation histograms, extracted binary features and their weights on
arbitrarily selected four pixels are shown in Fig. 3(c). In our study, the number
of generated images was 1,000 and the threshold value was 120. The votes were
concentrated on a few orientations at the pixels along lines or arcs such as
pixel (2) and (3). At these pixels the important features with large weights were
extracted. On the contrary, the votes were scattered among many orientations
at the pixels on corners and complicated structures such as pixel (1) and (4). At
these pixels the features with small or zero weihts were extracted. Features with
zero weights are not used for matching in pose estimation.

404 Y. Konishi et al.
Algorithm 1. Building hierarchical pose trees
Input: a number of PCOF templates T and their orientation histograms H
Output: hierarchical pose trees
T
0
← T
H
0
← H
i ← 1
loop
C
i
← cluster the templates in T
i−1
for each cluster C
ij
do
H
ij
← add histograms at each pixel of H
i−1
∈ C
ij
H
ij
← normalize histograms H
ij
T
ij
← thresholding H
ij
and extract new binary features and weights
end for
for each T
ij
and H
ij
do
H
ij
← add histograms of nearby 2 × 2 pixels
H
ij
← normalize histograms H
ij
T
ij
← thresholding H
ij
and extract new binary features and weights
end for
N
i
← minimum number of feature points in T
i
if N
i
<N
min
then
break
else
i ← i +1
end if
end loop
3.2 HPT: Hierarchical Pose Trees
A single PCOF template can handle the apparance changes caused by 3D pose
changes generated in training (±12
◦
around x-y axes, ±40 mm in the distance
and ±7.5
◦
around the optical axis). To cover a wider range of 3D object pose,
additional templates are made at every vertices of the viewpoint sphere in
Fig. 2(a) which contains 642 vertices as a whole and two adjacent vertices are
approximately 8
◦
apart. Additionally, the templates are made in every 30 mm in
the distance to the object and in every 5
◦
around the optical axes. These PCOF
templates can redundantly cover the whole 3D pose space.
Our proposed hierarchical pose trees (HPT) are built in a bottom-up way
starting from a lot of PCOF templates and their orientation histograms. The
algorithm is shown in Algorithm 1 and it consists of three steps: clustering, inte-
gration and reduction of resolutions. Firstly all the templates are clustered based
on the similarity scores (Eq. 2) between templates using X-means algorithms [34].
In X-means clustering, the optimum number of clusters are estimated based on
Bayesian information criteria (BIC). Secondly the orientation histograms which
belong to a same cluster are added and normalized at each pixel. Then the
clustered templates are integrated to new templates by extracting the binary
features and the weights from these integrated orientation histograms. Lastly
the resolutions of the histograms are reduced to half by adding and normalizing
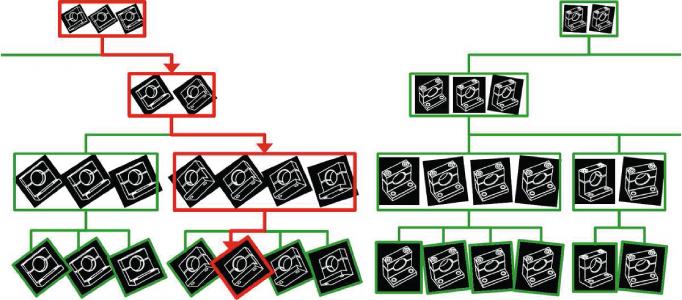
Fast 6D Pose Estimation Using Hierarchical Pose Trees 405
Fig. 4. Part of hierarchical pose trees are shown. Green and red rectangles repre-
sent templates used for matching. The bottom templates are originally created PCOF
templates and the tree structures are built in a bottom-up way by clustering simi-
lar templates, integrating them into new templates and decreasing the resolutions of
the templates. In estimation of object pose, HPT is traced from top to bottom along
the red line, and the most promising template which contains the pose parameters is
determined. (Color figure online)
histograms of neighboring 2 × 2 pixels. Then the low-resolution features and
weights are extracted from these histograms. These procedures are iterated until
the minimum number of feature points contained in low resolution templates is
less than a threshold value (N
min
). In our study N
min
was 50.
Part of HPT are shown in Fig. 4. When the range of 3D pose was as same
as the settings of experiment2 (±60
◦
around x-y axes, 660 mm – 800 mm in the
distance from the object and ±180
◦
around the optical axis), the total number of
PCOF templates amounted to 73,800 (205 viewpoints × 5 distances × 72 angles
around the optical axis). These initial templates were clustered and integrated
into 23,115 templates at the end of first round in Algorithm 1, and the number
of templates was further reduced to 4,269 at second round and to 233 at third
round. In this experimental settings, the iteration of hierarchization stopped at
third round.
3.3 6D Pose Estimation
In 6D pose estimation, firstly the image pyramid of a test image is built and the
quantized orientations are calculated on each pyramid level. Then the top level
of the pyramid is scanned using the root nodes of HPT (e.g. the number of root
nodes was 233 in experiment2). The similarity scores are calculated based on
Eq. 2. The promising candidates whose scores are higher than a search threshold
are matched with the templates at the lower levels, and they trace HPT down to
the bottom. Finally the estimated results of 2D positions on a test image and the
matched templates which have four pose parameters (three rotation angles and a

406 Y. Konishi et al.
distance) are obtained after non-maximum suppressions. 6D object pose of these
results are calculated by solving PnP problems based on the correspondences
between 2D feature points on the test image and 3D points of CAD data [35].
4 Experimental Results
We carried out two experiments. One is to evaluate the robustness of PCOF
against cluttered backgrounds and the appearance changes caused by the changes
in 3D object pose. Another is to evaluate the accuracy and the speed for our
combined PCOF and HPT to estimate 6D pose of texture-less objects.
4.1 Experiment1: Evaluation of Orientation Features
Experimental Settings. In experiment1, we evaluated four kinds of orien-
tation features on two test image sets (“vertical” and “perspective”) shown in
Fig. 5. A vertical image (a) was captured from the viewpoint on z-axis distanced
by 680 mm from the center of the object. The upper-left image in Fig. 2(b) is the
2D projection image of 3D CAD from the same viewpoint. Perspective images
(b) were captured from the same viewpoint as the vertical image with L-Holder
slightly rotated around x-y axes (approximately 8
◦
, please see Fig. 2(b) as ref-
erences). The number of the perspective images was eight (the combination of
+/0/− rotation around x-y axes) and these images contain almost the same
cluttered backgrounds. Our proposed PCOF was compared with three existing
orientation features: normalized gradient vector [23], spread orientation [8]and
cumulative orientation feature (COF) [26]. Existing methods used the upper-left
image in Fig. 2(b) as a model image.
Similarity scores based on four kinds of orientation features were calculated
at every pixel on the vertical and perspective images. We show the differences
between the maximum scores at the target object (FG: foreground) and at the
backgrounds (BG) in Table 1. This difference represents how discriminative each
feature is against cluttered backgrounds on the vertical image and is both against
cluttered backgrounds and changes in 3D object pose on the perspective images.
The larger the score difference is, the more discriminative the feature is. Regarding
the differences on the perspective images, mean values are presented in Table 1.
(a) (b)
Fig. 5. (a) Vertical image and (b) three examples of perspective images for evaluation
of the orientation features in experiment1. These images are almost identical except
for the 3D pose of the target object (L-Holder at the center of the images).

Fast 6D Pose Estimation Using Hierarchical Pose Trees 407
Table 1. Differences between a maximum score at the target object and at the back-
grounds on the vertical and perspective images in experiment1.
Steger [23] Spread [8] COF [26] PCOF(Ours)
Vertical 0.332 0.465 0.477 0.485
Perspective 0.214 0.421 0.403 0.483
Normalized Gradient Vector. Steger et al. [23] showed that the sum of
inner products of normalized gradient vectors was occlusion, clutter and illumi-
nation invariant. Our experimental results in Table 1 showed that the differences
between FG - BG scores both on the vertical and perspective images were much
lower than other three features. This demonstrated that Steger’s similarity score
was fragile both to the background clutters and to the changes in 3D object pose.
Spread Orientation. Hinterstoisser et al. [8] introduced the spread orientation
in order to make their similarity score robust to small shifts and deformations.
They efficiently spread the quantized orientations of test images by shifting the
orientation features over the range of ±4 ×±4 pixels and merging them with
bitwise OR operations. In our experimental results in Table 1, the difference
between FG - BG scores on the perspective images decreased from that on the
vertical image. This indicated that the spread orientation was robust to cluttered
backgrounds but not to the changes in 3D object pose.
Cumulative Orientation Feature (COF). Konishi et al. [26] introduced
COF, which was robust both to cluttered backgrounds and the appearance
changes caused by the changes in 2D object pose. Followoing their paper, we
generated many images by transformimg the model image using randomized
geometric transformation parameters (within the range of ±1 pixel in x-y trans-
lations, ±7.5
◦
of in-plane rotation and ±5 % of scale). Then COF was calculated
at each pixel by merging all the quantized orientations observed on generated
images. The COF template was matched with the test images and the results
were shown in Table 1. As with the spread orientation, the difference between
FG - BG scores on the perspective images was decreased and COF was robust
to cluttered backgrounds but not to the change in 3D object pose.
Perspectively Cumulated Orientation Feature (PCOF). PCOF was cal-
culated as described in Sect. 3.1 and matched with the quantized orientations
extracted on the test images. The difference between FG - BG scores in Table 1
were higher than other three features both on the vertical and perspective
images, and the score difference was not decreased on the perspective images
compared to that on the vertical image. This shows that PCOF was robust
both to cluttered backgrounds and the changes in 3D object pose. Due to this
robustness, the template which consist of PCOF can handle a certain range of
