
Experimental Liquidus Surface Projection
and Thermodynamic Modeling of the Fe-Mo-Nb
System
LEI ZOU, CUIPING GUO, CHANGRONG LI, and ZHENMIN DU
The liquidus surface projection of the Fe-Mo-Nb ternary system was constructed by means of
X-ray diffraction, scanning electron microscopy coupled with energy dispersive X-ray
spectroscopy, and differential thermal analysis. The experimental results indicate that the
liquidus surface projection consists of six primary soli dification regions and four ternary
invariant reactions. On the basis of the experimental results in the present work and isothermal
sections taken from the literature, the Fe-Mo-Nb system is modeled using the CALculation of
PHAse Diagram (CALPHAD) method. Solution phases, liquid, bcc, and fcc, are treated as the
substitutional solution. The l and Fe
2
(Mo, Nb) phases are treated as (Fe, Mo, Nb)
1
(Mo,
Nb)
4
(Fe, Mo, Nb)
2
(Fe, Mo, Nb)
6
and (Fe, Mo, Nb)
2
(Fe, Mo, Nb)
1
using the sublattice model,
respectively. A set of self-consistent thermodynamic parameters is thus obtained. The
experimental liquidus surface projection and isothermal sections at 900 C, 1100 C, and
1200 C are reproduced using the present thermodynamic description.
https://doi.org/10.1007/s11661-019-05254-5
The Minerals, Metals & Materials Society and ASM International 2019
I. INTRODUCTION
IN recent years, demand has increased for a broad
range of structural materials that are environmen tally
benign, energy efficient, light weight, and reliable in
design.
[1–3]
The next generation of high-pe rformance
structural materials, such as ultrastrong steel, must have
high strength/weight ratios, good fracture toughness,
and good joining capabilities.
[3]
The addition of molybdenum and niobium to steel
can effectively improve its strength and toughness.
[4,5]
Mo and Nb are strong carbide-forming elements in steel.
The carbides thus produced can obs truct the motion of
dislocations and prevent austenite grain growth during
austenization.
[4–10]
However, the addition of high con-
centrations of Mo can stabilize the r phase.
[11,12]
This
phase is extremely brittle, which leads to the formation
of cracks and causes the toughness of the steel to
deteriorate.
Phase diagrams provide the basic data needed when
designing material compositions and heat treatment
processes. Thus, it is impor tant to obtain the ternary
phase diagram for the Fe-Mo-Nb system to ensure the
correct development and design of new generations of
high-performance steels.
II. LITERATURE INFORMATION
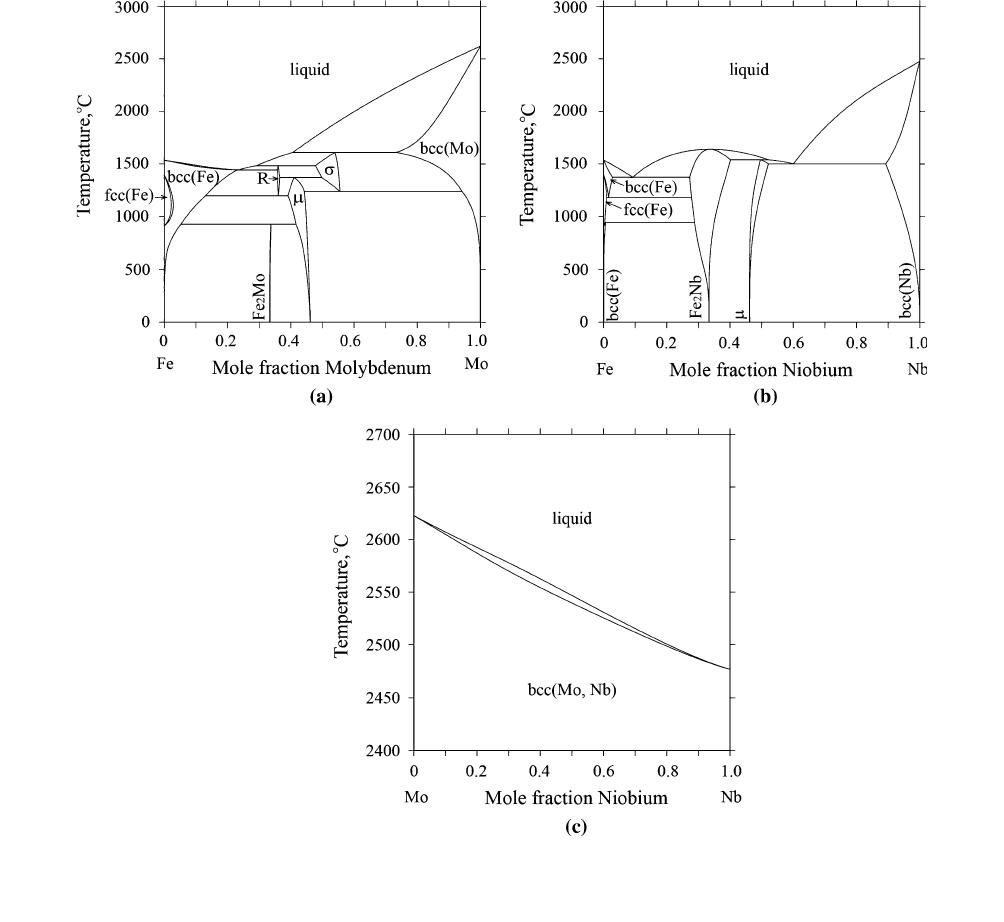
A. Binary Systems
Based on experimental data,
[13–20]
the Fe-Mo system
has been thermodynamically optimized by several
researchers.
[12,21–25]
The system has been subsequently
reassessed by Rajkumar and Kumar
[26]
based on their
experimental results and ab initio calculations . There-
fore, the updated thermodynamic description of the
Fe-Mo system provided by Rajkumar and Kumar
[26]
is
the one used in the present work.
The Fe-Nb system has also been optimized by many
researchers
[27–33]
based on the available experimental
investigations.
[34–40]
The optimization results of Jacob
et al.
[31]
were adopted by Guo et al.
[41]
and Stein et al.,
[42]
and the thermodynamic parameters from Reference 31
are also adopted in this work.
The Mo-Nb system has been optimized by Xiong
et al.
[43]
based on the experimental data obtained by
Kocherzhinskii and Vasilenko,
[44]
and their results are
the one adopted in this work.
The calculated Fe-Mo,
[26]
Fe-Nb,
[31]
and Mo-Nb
[43]
phase diagrams are shown in Figure 1.
LEI ZOU, CUIPING GUO, CHANGRONG LI, and ZHENMIN
DU are with the School of Materials Science and Engineering,
University of Science and Technology Beijing, Beijing 100083, P.R.
Manuscript submitted November 20, 2018.
Article published online May 3, 2019
3358—VOLUME 50A, JULY 2019 METALLURGICAL AND MATERIALS TRANSACTIONS A
B. Fe-Mo-Nb Ternary System
The first complete isothermal section at 900 C was
determined by Smirnova et al.,
[45]
and two three-phase
regions were constructed. The solubi lities of Mo in
l-Fe
7
Nb
6
and Nb in l-Fe
7
Mo
6
at 900 C were found to
be about 5 and 10 at. pct, respectively. Later on, the
Fe-rich (> 96 at. pct Fe) corners of the isothermal
sections at 950 C, 1050 C, 1150 C, and 1250 Cin
the Fe-Mo-Nb system were presented by Kumar and
Raghavan.
[46]
Recently, in some of our previous work, isothermal
sections at 1100 C and 1200 C were measured by
scanning electron microscopy coupled with energy
dispersive X-ray spectroscopy (SEM-EDS) and X-ray
diffraction (XRD).
[47]
It was found that there are four
three-phase regions in the isothermal section at 11 00 C
and three three-phase regions in the isothermal section
at 1200 C. The maximum solubilities of Mo in Fe
2
Nb
and l-Fe
7
Nb
6
, and Nb in l-Fe
7
Mo
6
were determined to
be about 26.97, 7.35, and 19.74 at. pct at 1100 C,
respectively. The corresponding maximum solubilities at
1200 C were determined to be about 25.08, 10.40, and
23.85 at. pct, respectively.
The main purpose of this work is to present the
self-consistent thermodynamic parameters for the indi-
vidual phases of the Fe-Mo-Nb system using the
CALPHAD (CALculation of PHAse Diagram) method.
Thermodynamic optimization is carried out based on
experiments. Due to a lack of experimental data related
to the liquid phases, the experimental liquidus surface
projection was determined by means of SEM-EDS,
XRD, and differential thermal analysis (DTA). The
liquidus surface projection constructed in the present
work an d the isothermal sections
[47]
help improve the
reliability of the available thermodynamic parameters.
Fig. 1—Calculated binary phase diagrams: (a) Fe–Mo
[26]
;(b) Fe–Nb
[31]
;(c) Mo–Nb
[43]
METALLURGICAL AND MATERIALS TRANSACTIONS A VOLUME 50A, JULY 2019—3359
III. EXPERIMENTAL PROCEDURES
High-purity starting materials were used to prepare
the ternary alloy samples in form of Fe bulk
(99.99 wt pct), Mo rods (99.99 wt pct), and Nb rods
(99.99 wt pct), in the present work. All samples were
prepared by arc-melting them under an argon atmo-
sphere of high purity. The arc furnace chamber was first
evacuated and flushed with pure Ar at least four times.
Then, a piece of pure Ti was re-melted at least three
times before alloying in order to consume any residual
oxygen. To ensure composition homogeneity, all sam-
ples were inverted and re-melted at least five times. The
ingots whose burning losses did not exceed 0.5 wt pct
were chosen to use in the subsequent experiments.
The as-cast microstructures and composition analyses
were carri ed out using a commercially available SEM
(LEO-1450, Zeiss, Germany) coupled with an EDS
(NORAN-7, Thermo Scientific, USA). An acceleration
voltage of 20 kV was employed. Composition measure-
ments were co nducted at least three times. The XRD
measurements were carried out using a diffractometer
(SmartLab, Rigaku, Japan) employing Cu-Ka radiation
(k = 1.5406 A
˚
) at 40kV and 150 mA. Diffraction spec-
tra were collected between 10 and 100 deg with a scan
step size of 0.02 deg.
The phase transformation temperatures at the Fe-rich
corner were determined by a DTA (SDT-Q600, TA Instru-
ments, USA) using Al
2
O
3
crucibles. The DTA measurements
were performed with heating rate of 10 Cmin
1
.
IV. THERMODYNAMIC OPTIMIZATION
A. Thermodynamic Model for Substitutional Phases
In the present work, Gibbs energy functions for the
unary phases (elemental Fe, Mo, and Nb) are taken
from the Scientific Group Thermodata Europe database
of pure elements compiled by Dinsdale.
[48]
In the Fe-Mo-Nb system, there are three solution
phases, liquid, fcc, and bcc. Their molar Gibbs energies
are described by the following expression:
G
/
m
ðTÞ¼x
Fe
G
/
Fe
ðTÞþx
Mo
G
/
Mo
ðTÞþx
Nb
G
/
Nb
ðTÞ
þ RTðx
Fe
ln x
Fe
þ x
Mo
ln x
Mo
þ x
Nb
ln x
Nb
Þ
þ
E
G
/
m
þ
mg
G
/
m
;
½1
where x
Fe
, x
Mo
, and x
Nb
are mole fractions of the pure
elements Fe, Mo, and Nb, respectively;
mg
G
/
m
is the
magnetic contribution to the free energy (vide infra)
and
E
G
/
m
is the excess Gibbs energy, which can be
expressed in the form of a Redlich–Kister polyn omial,
E
G
/
m
¼ x
Fe
x
Mo
X
n
n
L
/
Fe;Mo
ðx
Fe
x
Mo
Þ
n
þ x
Fe
x
Nb
X
n
n
L
/
Fe;Nb
ðx
Fe
x
Nb
Þ
n
þ x
Mo
x
Nb
X
n
n
L
/
Mo;Nb
ðx
Mo
x
Nb
Þ
n
þ x
Fe
x
Mo
x
Nb
L
/
Fe;Mo;Nb
; ½2
where
n
L
/
Fe;Mo
,
n
L
/
Fe;Nb
, and
n
L
/
Mo;Nb
are the nth inter-
action parameters between elements Fe and Mo, Fe and
Nb, and Mo an d Nb, respectively, which can be taken
from References 26, 31, and 43. L
/
Fe;Mo;Nb
is the ternary
interaction parameter which we express in the form:
L
/
Fe;Mo;Nb
¼ x
Fe
0
L
/
Fe;Mo;Nb
þ x
Mo
1
L
/
Fe;Mo;Nb
þ x
Nb
2
L
/
Fe;Mo;Nb
; ½3
where
n
L
/
Fe;Mo;Nb
are the parameters to be optimized in
the present work.
In the Fe-Mo and Fe-Nb systems, there is a magnetic
contribution to the Gibbs energy in the fcc and bcc
phases. The model of magnetic contribution to the
Gibbs energy
mg
G
/
m
was proposed by Inden
[49]
and
modified by Hillert and Jarl,
[50]
and
mg
G
/
m
is expressed as
follows:
mg
G
/
m
¼ RTIn b þ 1ðÞf sðÞ; ½4
where f sðÞis the polynomial function obtained by Hil-
lert and Jarl
[50]
based on the magnetic specific heat of
iron which is defined in terms of s = T/T
c
where T
c
is
the Curie temperature, and b is the average atomic
magnetic moment (set equal to the molar Bohr mag-
netic moment). The parameters T
c
and b can be
described using the following expressions:
T
/
c
¼ x
Fe
T
/
cFe
þ x
Mo
T
/
cMo
þ x
Nb
T
/
cNb
þ x
Fe
x
Mo
X
n
n
T
/
cFe;Mo
ðx
Fe
x
Mo
Þ
n
þ x
Fe
x
Nb
X
n
n
T
/
cFe;Nb
ðx
Fe
x
Nb
Þ
n
þ x
Mo
x
Nb
X
n
n
T
/
cMo;Nb
ðx
Mo
x
Nb
Þ
n
þ x
Fe
x
Mo
x
Nb
T
/
cFe;Mo;Nb
½5
b
/
¼ x
Fe
b
/
Fe
þ x
Mo
b
/
Mo
þ x
Nb
b
/
Nb
þ x
Fe
x
Mo
X
n
n
b
/
Fe;Mo
ðx
Fe
x
Mo
Þ
n
þ x
Fe
x
Nb
X
n
n
b
/
Fe;Nb
ðx
Fe
x
Nb
Þ
n
þ x
Mo
x
Nb
X
n
n
b
/
Mo;Nb
ðx
Mo
x
Nb
Þ
n
þ x
Fe
x
Mo
x
Nb
b
/
Fe;Mo;Nb
; ½6
where T
/
c
and b
/
are the corresponding magnetic
parameters of pure elements Fe, Mo, and Nb;
n
T
/
c;
and
n
b
/
;
are the nth binary magnetic interaction parameters;
T
/
cFe;Mo;Nb
and b
/
Fe;Mo;Nb
are the ternary magnetic inter-
action parameters. All the magnetic parameters except
T
/
cFe
and b
/
Fe
were set to zero due to a lack of
experimental data on the magnetic properties of the
binary and ternary bcc and fcc solutions.
3360—VOLUME 50A, JULY 2019 METALLURGICAL AND MATERIALS TRANSACTIONS A

B. Thermodynamic Model for Intermetallic Phases
The tw o intermetallic compounds Fe
2
Mo and Fe
2
Nb
are treated as one phase and referred to as Fe
2
(Mo, Nb)
because they have same crystal structure (that of
MgZn
2
). Similarly, the l-Fe
7
Nb
6
and l-Fe
7
Mo
6
phases
are treated as one phase l. In the present optimization
work, the thermodynamic models of Fe
2
(Mo, Nb) and l
are treated as (Fe, Mo, Nb)
2
(Fe, Mo, Nb)
1
and (Fe, Mo,
Nb)
1
(Mo, Nb)
4
(Fe, Mo, Nb)
2
(Fe, Mo, Nb)
6
, respec-
tively. The models of R and r phases are Fe
32
Mo
18
(Fe,
Mo)
3
and (Fe, Mo)
10
(Fe, Mo)
20
, respectively, which are
from Reference 26.
In the Fe-Mo-Nb system, there is no magnetic contribu-
tion to the Gibbs energy of the intermetallic compounds.
Taking Fe
2
(Mo, Nb) as an example, the Gibbs energies per
mole of formula unit Fe
2
(Mo, Nb) is expressed as
G
Fe
2
Mo;NbðÞ
¼
X
i
X
j
y
0
i
y
00
j
G
Fe
2
Mo;NbðÞ
i:j
þ RT 2
X
i
y
0
i
Iny
0
i
þ
X
i
y
00
i
Iny
00
i
!
þ
X
i
X
j
X
k
y
0
i
y
0
j
y
00
k
n
L
Fe
2
Mo;NbðÞ
i;j:k
þ
X
i
X
j
X
k
y
0
i
y
00
j
y
00
k
n
L
Fe
2
Mo;NbðÞ
i:j;k
; ½7
where the dummy variables i, j,andk represent Fe, Mo,
and Nb. Parameters y
0
i
and y
0
j
are the site fractions of i
and j on the first sublattice, respectively, and y
00
j
and y
00
k
are the site fractions of j and k on the second sublattice,
respectively. Also, G
Fe
2
Mo;NbðÞ
i:j
is the Gibbs energy of the
end-members i
2
j,
n
L
Fe
2
Mo;NbðÞ
i;j:k
is the nth interaction
parameter between i and j on the first sublattice when
the second sublattice is occupied by element k.
n
L
Fe
2
Mo;NbðÞ
i:j;k
is the nth interaction parameter between j
and k on the second sublattice when the first sublattice is
occupied by i element.
C. Assessment Procedur e
Optimization was carried out using the PARROT
module in the software package Thermo-Calc,
[51]
which
is capable of handing various kinds of experimental
data. The program works by mini mizing an error sum
wherein each of the selected data values is given a
certain weight. The step-by-step modeling procedure
described by Du et al.
[52]
was utilized in the present
optimizations performed in this work. The intermet allic
compounds were optimized first based on the experi-
mental results. Then, the parameters for the solution
phases were optimized. Subsequently, the parameters
Table I. Compositions and Primary Solidification Phases of the As-Cast Fe-Mo-Nb Alloys
No.
Alloy Compositions (At Pct)
Primary Solidification Phase
Phase Compositions (At Pct)
Phase 2 Phase 3Fe Mo Nb Fe Mo Nb
#1 94.5 3.3 2.2 bcc(Fe) 93.1 3.7 3.2 Fe
2
(Mo, Nb) —
#2 90.8 6.2 3.0 bcc(Fe) 88.2 10.0 1.8 Fe
2
(Mo, Nb) —
#3 85.7 9.1 5.2 bcc(Fe) 86.9 11.2 1.9 Fe
2
(Mo, Nb) —
#4 82.9 13.2 3.9 bcc(Fe) 87.0 10.7 2.3 Fe
2
(Mo, Nb) —
#5 65.6 33.0 1.4 r 52.8 42.9 4.3 l bcc(Fe)
#6 61.7 35.2 3.1 r 51.9 43.0 5.1 l bcc(Fe)
#7 82.5 5.0 12.5 Fe
2
(Mo, Nb) 65.2 6.7 28.1 bcc(Fe) —
#8 78.0 12.5 9.5 Fe
2
(Mo, Nb) 67.9 5.2 26.9 bcc(Fe) —
#9 73.8 9.9 16.3 Fe
2
(Mo, Nb) 66.1 8.1 25.8 bcc(Fe) —
#10 69.2 16.7 13.8 Fe
2
(Mo, Nb) 65.1 14.8 20.1 l bcc(Fe)
#11 64.8 10.3 24.9 Fe
2
(Mo, Nb) 64.3 8.6 27.1 l bcc(Fe)
#12 62.1 16.8 21.1 Fe
2
(Mo, Nb) 62.1 16.5 21.4 l bcc(Fe)
#13 59.7 8.1 32.2 Fe
2
(Mo, Nb) 56.4 3.4 40.2 l —
#14 54.9 12.2 32.9 Fe
2
(Mo, Nb) 55.4 4.7 39.9 l —
#15 49.5 3.8 46.7 Fe
2
(Mo, Nb) 59.9 1.2 38.9 l bcc(Mo, Nb)
#16 74.3 23.2 2.5 l 57.2 35.1 7.7 bcc(Fe) Fe
2
(Mo, Nb)
#17 73.1 20.2 6.7 l 60.2 32.1 7.8 bcc(Fe) Fe
2
(Mo, Nb)
#18 71.1 26.5 2.4 l 58.5 37.2 4.3 bcc(Fe) Fe
2
(Mo, Nb)
#19 67.5 23.2 9.3 l 57.9 32.2 9.9 bcc(Fe) Fe
2
(Mo, Nb)
#20 65.6 28.3 6.1 l 57.3 34.5 8.2 bcc(Fe) Fe
2
(Mo, Nb)
#21 61.2 28.1 10.7 l 58.7 34.6 6.7 bcc(Fe) Fe
2
(Mo, Nb)
#22 60.9 23.6 15.5 l 57.3 32.5 10.2 bcc(Fe) Fe
2
(Mo, Nb)
#23 56.6 21.6 21.8 l 53.1 28.8 18.1 Fe
2
(Mo, Nb) —
#24 44.8 1.7 53.5 l 50.3 3.7 46.0 bcc(Mo, Nb) —
#25 56.3 41.3 2.4 bcc(Mo, Nb) 15.8 71.7 12.5 rl
#26 48.5 33.1 18.4 bcc(Mo, Nb) 6.6 62.5 30.9 l —
#27 46.2 17.3 36.5 bcc(Mo, Nb) 6.8 50.4 42.8 l —
#28 40.9 7.9 51.2 bcc(Mo, Nb) 6.1 16.0 77.9 l —
#29 40.4 28.4 31.2 bcc(Mo, Nb) 8.2 45.8 46.0 l —
#30 30.8 21.6 47.6 bcc(Mo, Nb) 6.11 27.1 66.8 l —
#31 29.1 48.5 22.4 bcc(Mo, Nb) 8.2 54.8 37.0 l —
METALLURGICAL AND MATERIALS TRANSACTIONS A VOLUME 50A, JULY 2019—3361
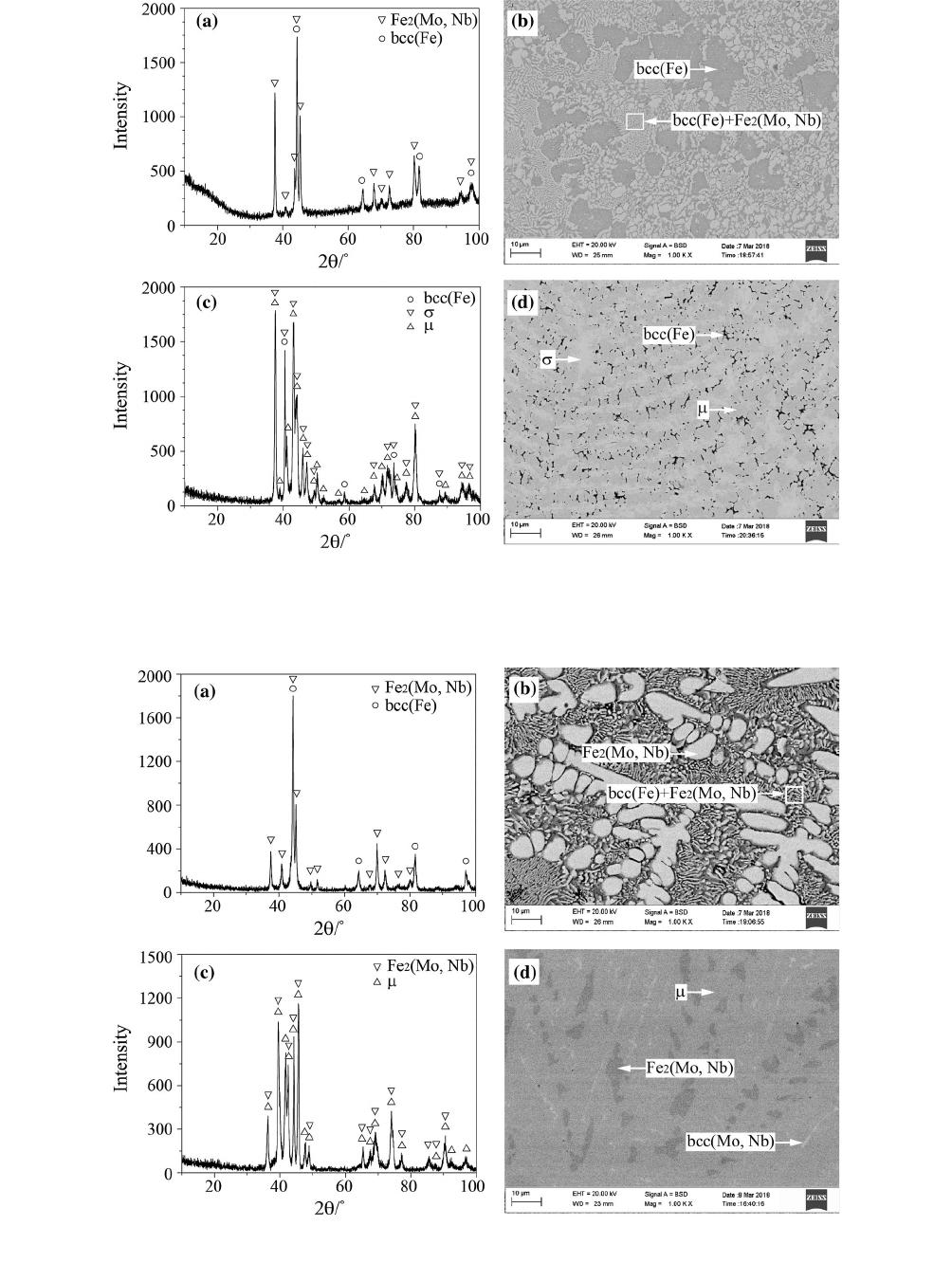
Fig. 2—XRD patterns and BSE micrographs: (a) and (b) for alloy #4; (c) and ( d) for alloy #5.
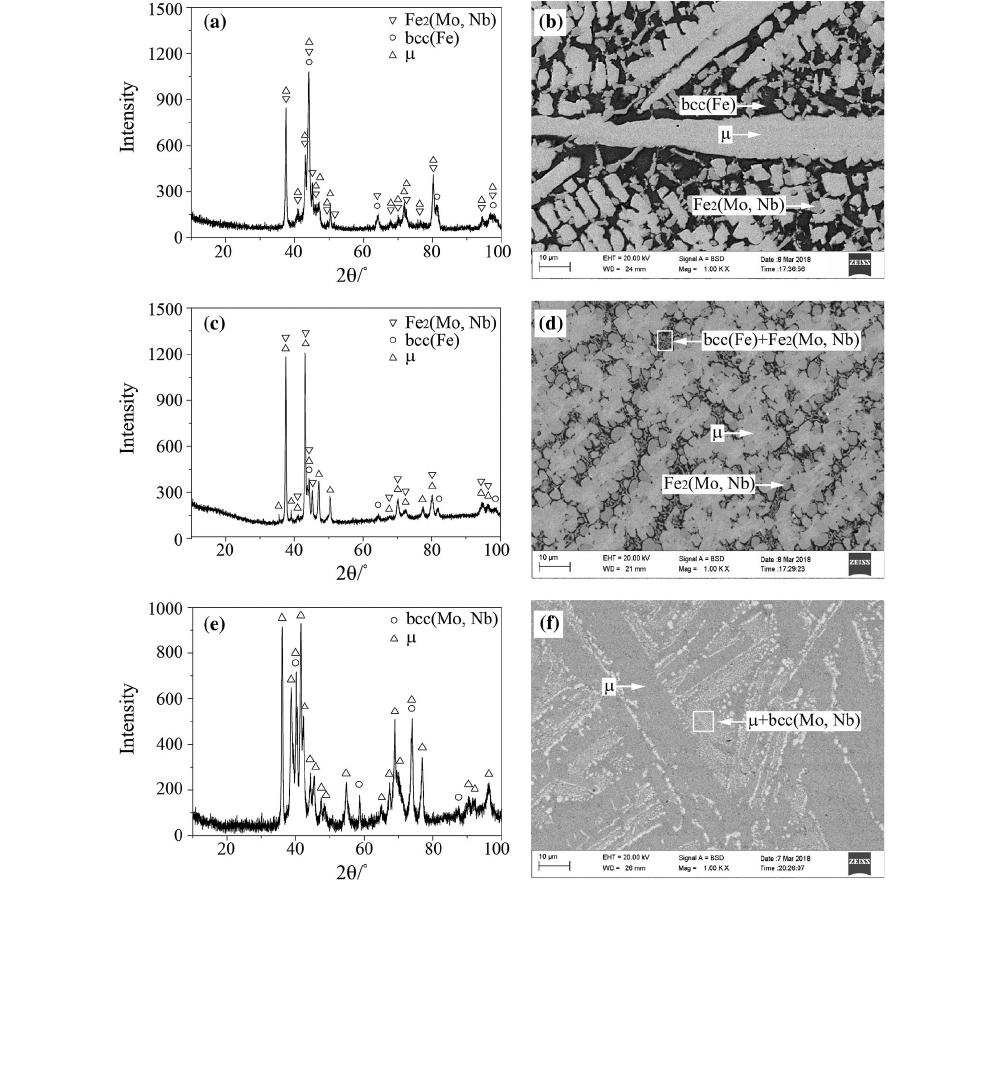
Fig. 3—XRD patterns and BSE micrographs: (a) and (b) for alloy #8; (c) and ( d) for alloy #15.
3362—VOLUME 50A, JULY 2019 METALLURGICAL AND MATERIALS TRANSACTIONS A
for the liquid phase were evaluated also based on
experimental results. Greater weights were given to the
experimental data for the isothermal sections
[47]
and the
present liquidus surface projection. Finally, all the
parameters were optimized concurrently to achieve a
set of self-consistent thermodynamic parameters.
Based on the experimental liquidus surfa ce projection
in this work and the isothermal sections from the
literature, the thermodynamic parameters for the indi-
vidual phases in the Fe-Mo-Nb system were all
optimized.
V. RESULTS AND DISCUSSION
A. Experimental Liquidus Surface Projection
To investigate the liquidus surface projection of the
Fe-Mo-Nb system, 31 alloy samples were prepared. The
compositions and primary solidification phases of the
as-cast alloys are summarized in Table I.
The primary solidification phase bcc(Fe) is observed
in alloys #1 to #4. Figures 2(a) and (b) show the XRD
pattern and backscattered electron (BSE) micrograph
obtained for alloy #4, respectively. The XRD pattern
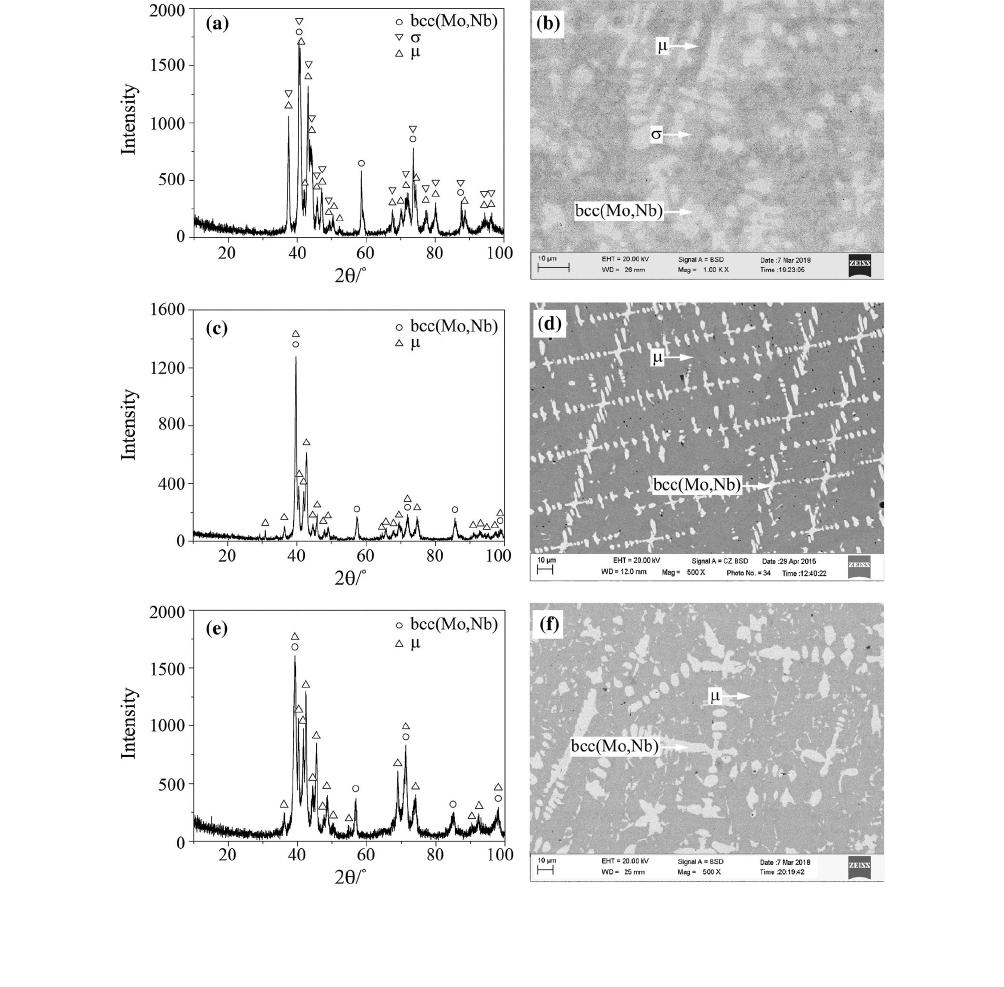
Fig. 4—XRD patterns and BSE micrographs: (a) and (b) for alloy #16; (c) and (d) for alloy #19; (e) and (f) for alloy #24.
METALLURGICAL AND MATERIALS TRANSACTIONS A VOLUME 50A, JULY 2019—3363
only contains diffraction peaks corresponding to bcc(Fe)
and Fe
2
(Mo, Nb), and two typical microstructures are
observed in alloy #4. The bulk gray microstr ucture is the
primary solidification phase bcc(Fe) (Fe—10.7 at. pct
Mo—2.3 at. pct Nb), and the lamellar microstructure
corresponds to a eutectic mixture of bcc(Fe) + Fe
2
(Mo,
Nb). The solidification path of alloy #4 is presumed
to be as follows: liq. fi bcc(Fe), liq. fi bcc(Fe) +
Fe
2
(Mo, Nb).
For alloys #5 and #6, the primary solidification phase
is r. The XRD pattern and BSE micrograph of alloy #5
are shown in Figures 2 (c) and (d), respectively. The
bright phase is the primary solidification phase r
(Fe—42.9 at. pct Mo—4.3 at. pct Nb). The r phase
precipitates from liquid during the solidification process
of alloy #5, and the liquid composition reaches the
monovariant line (liq. + r fi l). The l phase is form ed
around the r phase and hinders the further reaction
between the liquid and r phase, resulting in the liquid
composition crosses over the monovariant line (liq. +
r fi l) and the l phase solidifies directly from
liquid. At the end of the solidification process, the black
linear bcc(Fe) is formed by the eutectic reaction
liq. fi l + bcc(Fe).
Alloys #8 to #15 are located in the primary solidifi-
cation region of Fe
2
(Mo, Nb). According to the XRD
pattern and microstructure of alloy #8 shown in
Figures 3(a) and (b), the bright phase is the primary
solidification phase Fe
2
(Mo, Nb) (Fe—5.2 at. pct,
Mo—26.9 at. pct Nb), and the lamellar microstructure
Fig. 5—XRD patterns and BSE micrographs: (a) and (b) for alloy #25; (c) and (d) for alloy #27; (e) and (f) for alloy #28.
3364—VOLUME 50A, JULY 2019 METALLURGICAL AND MATERIALS TRANSACTIONS A
is a eutectic with microstructure of bcc(Fe) + Fe
2
(Mo,
Nb). The XRD pattern and BSE micrograph of alloy
#15 are shown in Figures 3(c) and (d), respectively.
Combining the results of XRD and EDS, the dark and
gray phase are Fe
2
(Mo, Nb) and l, respectively. The
white phase cannot be determined due to its low
content. The composition of alloy #15 is close to the
Fe-Nb side. Therefore, the Fe
2
(Mo, Nb) phase first
precipitates from liquid during the solidification process ,
and the liquid composition reaches the monovariant line
(liq. + Fe
2
(Mo, Nb) fi l). The l phase is formed
around Fe
2
(Mo, Nb) and hinders the further reaction
between liquid and Fe
2
(Mo, Nb), resulting in the liquid
composition crosses over the monovariant line (liq.+-
Fe
2
(Mo, Nb) fi l) and the l phase solidifies directly
from liquid. According to the imaging principle of back
scattered electron, the small amount of white phase is
the bcc(Mo, Nb) phase. So, the liquid composition
finally reaches the monovariant line (liq. fi l +
bcc(Mo, Nb)).
The primary solidification phase l is observed in
alloys #16 to #24. The XRD pattern and BSE micro-
graph of alloy #16 are shown in Figures 4(a) and (b),
respectively. The gray phase is the primary solidification
phase l (Fe—35.1 at. pct Mo—7.7 at. pct Nb). The
black and dark gray phases are bcc(Fe) and Fe
2
(Mo,
Nb), respectively. The XRD pattern and BSE micro-
graph of alloy #19 are shown in Figures 4(c) and (d),
respectively. The bright pha se is determined to be the
primary solidification phase l (Fe—32.2 at. pct
Mo—9.9 at. pct Nb), and the gray phase is Fe
2
(Mo,
Nb) (Fe—12.0 at. pct Mo—20.9 at. pct Nb). The lamel-
lar microstructure is the eutectic microstructure of
bcc(Fe) + Fe
2
(Mo, Nb).
Unlike alloys #16 and #19, the XRD pattern of alloy
#24 shown in Figure 4(e) confirms the existence of the
l and bcc(Mo, Nb) phases. The gray phase is the
primary solidification phase l (Fe—3.7 at. pct
Mo—46.0 at. pct Nb), and the lamellar microstructure
is the eutectic microstructure of l+bcc(Mo, Nb). The
composition of alloy #24 is close to the Fe-Nb side.
According to the Fe-Nb phase diagram, the composi-
tion of the liquid inevitably reaches the monovariant
line (liq. fi l + bcc(Mo, Nb)) with decreasing tem-
perature. Therefor e, the microstructures of the primary
solidification phase l and eutectic l+bcc(Mo, Nb) are
observed in alloy #24.
Alloys #25 to #31 are located in the primary
solidification region of bcc(Mo, Nb). The XRD pattern
and BSE micrograph of alloy #25 are shown in
Figures 5(a) and (b), respectively. The bright phase is
determined to be bcc(Mo, Nb) (Fe—71.7 at. pct
Mo—12.5 at. pct Nb). The gray phase around the
bcc(Mo, Nb) phase is r which is formed by the reactions
liq.+bcc(Mo, Nb) fi r and liq. fi r. The dark gray
phase is l which precipitates due to the peritectic
reaction liq. + r fi l. Unlike alloy #25, bright den-
dritic microstructures can be clearly observed in
Figures 5(d) and (f). Combining the experimental results
obtained using XRD and EDS, the bright primary
solidification phase corresponds to bcc(Mo, Nb).
In the present work, the primary solidification phase
R is not observed in any of the alloys.
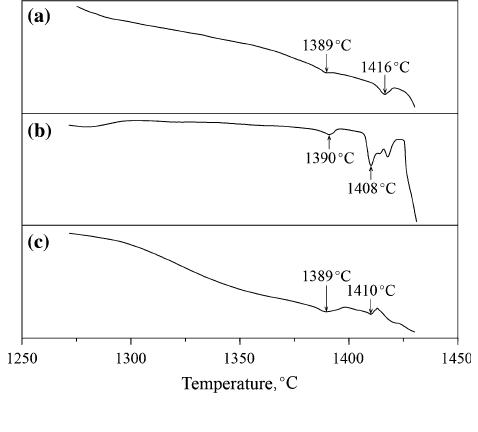
The DTA curves for a lloys #16 to #18 are shown in
Figure 6. A phase transformation peak with an onset at
1389 C can be observed in the DTA curves. According
to the experimental analysis, alloys #16 to #18 have the
same reaction in the solidification process, namely
liq. + l fi bcc(Fe) + Fe
2
(Mo, Nb). Therefore, it can
be deduced that the temperature 1389 C corresponds to
the invariant reaction liq. + l fi bcc(Fe) + Fe
2
(Mo,
Nb). Due to the temperature limitations of the DTA
instrument (SDT-Q600, TA Instruments, USA), only
the temperature of the invariant reaction liq. + l
fi bcc(Fe) + Fe
2
(Mo, Nb) is determined.
The above experimenta l results were subsequently
used to construct the liquidus surface projection of the
Fe-Mo-Nb system.
B. Thermodynamic Calculations
The thermodynamic parameters obtained for the
Fe-Mo-Nb system in the present work are listed in
Table II, and the calculated invariant reactions in the
Fe-Mo-Nb system are shown in Table III. It can be seen
that the temperature of invariant reaction U
4
is in
agreement with the DTA results in the present work.
Figure 7 shows the liquidus surface projection calcu-
lated for the Fe-Mo-Nb system using the present
thermodynamic descriptions and present experimental
data. Satisfactory agreement can be seen to have been
obtained between the calculated results and experimen-
tal data. The complete reaction scheme predicted for the
Fe-Mo-Nb system is shown in Figure 8.
Fig. 6—DTA curves of alloys: (a) #16; (b) #17; (c) #18.
METALLURGICAL AND MATERIALS TRANSACTIONS A VOLUME 50A, JULY 2019—3365

Table II. Thermodynamic Parameters in the Fe-Mo-Nb System
Phase Thermodynamic Parameters Refs.
Liquid model (Fe, Mo, Nb)
1
0
L
liquid
Fe;Mo
¼11712 þ 2:917T 26
0
L
liquid
Fe;Nb
¼74257 þ 99:67T 10T lnðTÞ 31
1
L
liquid
Fe;Nb
¼þ17624 10:805T 31
0
L
liquid
Mo;Nb
¼þ15253:7 43
1
L
liquid
Mo;Nb
¼þ10594 43
0
L
liquid
Fe;Mo;Nb
¼26580 :11 this work
1
L
liquid
Fe;Mo;Nb
¼145201:38 this work
2
L
liquid
Fe;Mo;Nb
¼88271 :81 this work
fcc model (Fe, Mo, Nb)
1
(Va)
1
0
L
fcc
Fe;Mo
¼þ20978 11:843T 26
0
L
fcc
Fe;Nb
¼6176 2:04T 31
T
fcc
cFe
¼201 43
b
fcc
Fe
¼2:10 43
0
L
fcc
Fe;Mo;Nb
¼þ151251:49 this work
bcc model (Fe, Mo, Nb)
1
(Va)
3
0
L
bcc
Fe;Mo
¼þ38849 9:539T 26
1
L
bcc
Fe;Mo
¼8988 26
0
T
bcc
cFe;Mo
¼þ334 26
1
T
bcc
cFe;Mo
¼þ531 26
0
L
bcc
Fe;Nb
¼10893 þ 10:288T 31
1
L
bcc
Fe;Nb
¼þ4674 5:776T 31
0
L
bcc
Mo;Nb
¼68202 þ 29:8559T 43
1
L
bcc
Fe;Nb
¼þ8201:3 43
T
bcc
cFe
¼þ1043 43
b
bcc
Fe
¼þ2:22 43
1
L
bcc
Fe;Mo;Nb
¼46852 :12 þ 30:0253T this work
2
L
bcc
Fe;Mo;Nb
¼56564 :96 þ 33:7643T this work
R model Fe
32
Mo
18
(Fe, Mo)
3
G
R
Fe:Mo:Fe
= 35GHSER
Fe
+ 18GHSER
Mo
þ 50909 177:308T 26
G
R
Fe:Mo:Mo
¼ 32GHSER
Fe
þ21GHSER
Mo
91498 83:151T 26
r model (Fe, Mo)
10
(Fe, Mo)
20
G
r
Fe:Fe
¼ 30GHSER
Fe
þ 226500 26
G
r
Mo:Fe
¼ 20GHSER
Fe
þ10GHSER
Mo
þ 487900 26
G
r
Fe:Mo
= 10GHSER
Fe
þ20GHSER
Mo
þ 31407 43:882T 26
G
r
Mo:Mo
¼ 30GHSER
Mo
þ 486900 26
0
L
r
Fe:Fe;Mo
¼48114 26
Fe
2
(Mo, Nb) model (Fe, Mo, Nb)
2
(Fe, Mo, Nb)
1
G
Fe
2
Mo;NbðÞ
Fe:Fe
= 3GHSER
Fe
þ 44130 26,31
G
Fe
2
Mo;NbðÞ
Fe:Mo
= 2GHSER
Fe
+ GHSER
Mo
20443 þ 7:289T 26
G
Fe
2
Mo;NbðÞ
Mo:Fe
¼ GHSER
Fe
+ 2GHSER
Mo
þ 50443 7:289T 26
3366—VOLUME 50A, JULY 2019 METALLURGICAL AND MATERIALS TRANSACTIONS A

Table II. continued
Phase Thermodynamic Parameters Refs.
G
Fe
2
Mo;NbðÞ
Mo:Mo
¼ 3GHSER
Mo
þ 15000 26
0
L
Fe
2
Mo;NbðÞ
Fe:Fe;Mo
¼þ70000 26
0
L
Fe
2
Mo;Nb
ðÞ
Fe;Mo:Mo
¼þ59450 26
G
Fe
2
Mo;NbðÞ
Fe:Nb
¼ 2GHSER
Fe
+ GHSER
Nb
67223 þ 13:971T 31
G
Fe
2
Mo;NbðÞ
Nb:Fe
¼ GHSER
Fe
+ 2GHSER
Nb
þ 180030 31
G
Fe
2
Mo;NbðÞ
Nb:Nb
¼ 3GHSER
Nb
þ 49620 31
0
L
Fe
2
Mo;NbðÞ
Fe:Fe;Nb
¼
0
L
Fe
2
Mo;NbðÞ
Nb:Fe;Nb
¼33816 31
G
Fe
2
Mo;NbðÞ
Mo:Nb
¼ 2GHSER
Mo
+ GHSER
Nb
þ 49750:41 this work
G
Fe
2
Mo;NbðÞ
Nb:Mo
¼ GHSER
Mo
+ 2GHSER
Nb
þ 95248:29 this work
0
L
Fe
2
Mo;NbðÞ
Fe:Mo;Nb
¼þ17917:52 16:4472T this work
1
L
Fe
2
Mo;NbðÞ
Fe:Mo;Nb
¼þ42452:16 30:4231T this work
0
L
Fe
2
Mo;NbðÞ
Fe:Fe;Mo;Nb
¼100132:03 this work
l model (Fe, Mo, Nb)
1
(Mo, Nb)
4
(Fe, Mo, Nb)
2
(Fe, Mo, Nb)
6
G
l
Fe:Mo:Fe:Fe
¼ 9GHSER
Fe
+ 4GHSER
Mo
þ 74090 76:677T 26
G
l
Fe:Mo:Fe:Mo
¼ 3GHSER
Fe
+ 10GHSER
Mo
þ 445950 26
G
l
Fe:Mo:Mo:Fe
¼ 7GHSER
Fe
+ 6GHSER
Mo
68875 þ 8:955T 26
G
l
Fe:Mo:Mo:Mo
¼ GHSER
Fe
+ 12GHSER
Mo
þ 340960 26
G
l
Mo:Mo:Fe:Fe
¼ 8GHSER
Fe
+ 5GHSER
Mo
þ 100890 26
G
l
Mo:Mo:Fe:Mo
¼ 2GHSER
Fe
+ 11GHSER
Mo
þ 484770 26
G
l
Mo:Mo:Mo:Fe
¼ 6GHSER
Fe
+ 7GHSER
Mo
þ 23550 26
G
l
Mo:Mo:Mo:Mo
¼ 13GHSER
Mo
þ 394940 26
0
L
l
Fe:Mo:Fe;Mo:Fe
¼137510 þ 105:096T 26
G
l
Fe:Nb:Fe:Fe
¼ 9GHSER
Fe
+ 4GHSER
Nb
100230 31
G
l
Nb:Nb:Fe:Fe
¼ 8GHSER
Fe
+ 5GHSER
Nb
27430 31
G
l
Fe:Nb:Nb:Fe
¼ 7GHSER
Fe
+ 6GHSER
Nb
266116 þ 56T 31
G
l
Nb:Nb:Nb:Fe
¼ 6GHSER
Fe
+ 7GHSER
Nb
131400 31
G
l
Fe:Nb:Fe:Nb
¼ 3GHSER
Fe
+ 10GHSER
Nb
þ 426530 31
G
l
Nb:Nb:Fe:Nb
¼ 2GHSER
Fe
+ 11GHSER
Nb
þ 499200 31
G
l
Fe:Nb:Nb:Nb
¼ GHSER
Fe
+ 12GHSER
Nb
þ 176020 31
G
l
Nb:Nb:Nb:Nb
¼ 13GHSER
Nb
þ 227500 31
G
l
Fe:Mo:Nb:Fe
¼ 7GHSER
Fe
+ 4GHSER
Mo
+ 2GHSER
Nb
146415:80þ10:0590T
this work
G
l
Fe:Nb:Mo:Fe
¼ 7GHSER
Fe
+ 2GHSER
Mo
+ 4GHSER
Nb
85904:30þ13:9406T this work
G
l
Mo:Nb:Nb:Fe
¼ 6GHSER
Fe
+ GHSER
Mo
+ 6GHSER
Nb
this work
G
l
Nb:Mo:Nb:Fe
¼ 6GHSER
Fe
+ 4GHSER
Mo
+ 3GHSER
Nb
this work
G
l
Nb:Nb:Mo:Fe
¼ 6GHSER
Fe
+ 2GHSER
Mo
+ 5GHSER
Nb
this work
G
l
Fe:Mo:Fe:Nb
¼ 3GHSER
Fe
+ 4GHSER
Mo
+ 6GHSER
Nb
this work
G
l
Fe:Nb:Fe:Mo
¼ 3GHSER
Fe
+ 6GHSER
Mo
+ 4GHSER
Nb
this work
G
l
Fe:Nb:Mo:Mo
¼ GHSER
Fe
+ 8GHSER
Mo
+ 4GHSER
Nb
this work
G
l
Fe:Mo:Nb:Nb
¼ GHSER
Fe
+ 4GHSER
Mo
+ 8GHSER
Nb
this work
METALLURGICAL AND MATERIALS TRANSACTIONS A VOLUME 50A, JULY 2019—3367
