Chapter 6

Magnetic Flux Leakage Testing

6.1 Introduction

As early as 1868, the British Naval Architects Association began to use magnetic

ﬂux leakage technology and found defects on steel pipe through the compass. In

1918, it was found that powder was absorbed near defects due to the changes in

surface magnetic ﬁeld; thus, magnetic particle detection method was invented. After

continuous development, the magnetic ﬂux leakage testing technology not only can

detect the defects, but also can analyze the characteristics of the defects [1, 2].

In the theoretical analysis of magne tic leakage ﬁeld, it can be divided into

analytical method and numerical method. In 1966, Zatsepin and Shcherbinin were

the ﬁrst to put forward the analytical equation of the magnetic ﬂux leakage ﬁeld of

inﬁnite long rectangular crack, as shown in Fig. 6.1 [3]. Based on the theoretical

model, the magnetic ﬂux leakage ﬁeld can be generated by a dipole with two

opposite polars. Taking the hole defect in the two-dimensional space as an example,

the two magnetic poles are assigned to the two sides of the defect. The magnetic

charge densities of the two poles are −Q and +Q, respectively. So, the magnetic ﬂux

leakage of the defect in point P(x, y) is given as follows:

¼ B

!

þ B

!

Q

4pl

ð6:1Þ

Among them, μ

is the vacuum permeability. The holes, pits, and other defects

on the surface of the workpiece can be simulated by the equivalent point dipole

model. For the crack defect, it should be equivalent to the rectangular groove,

whose length is inﬁnite, and then, the equivalent surface dipole model is used to

simulate the crack.

Using the dipole model, the authors calculated the magnetic leakage ﬁeld of

inﬁnite long cracks in the surface [3]. After that, the magnetic ﬁeld distribution of the

ﬁnite length cracks in the surface was calculated by Shcherbinin and Pashagin [4].

S. Huang and S. Wang, New Technologies in Electromagnetic Non-destructive Testing,

Springer Series in Measurement Science and Technology,

DOI 10.1007/978-981-10-0578-7_6

185

However, they did not connect the strength of the magnetic leakage ﬁeld to the

strength of the magnetizing ﬁeld and the permeability. They used two-dimensional

models. The main progress of the analytical met hod of magnetic leakage ﬁeld analysis

was completed by Edwards and Palmer in 1986 [5]. They perfected the magnetic

dipole model. The shape parameters of the defect, the magnetizing ﬁeld strength, the

permeability, and the magnetic ﬂux leakage of the material were ﬁrstly connected.

The limitation of Edwards and Palmer’s model was that the permeability of the

material was supposed as a linear parameter in the derivation process. So there were

some errors between the theoretical results and the experimental results.

Therefore, numerical calculation method is usually adopted. The numerical cal-

culation method overcomes the limitation of the magnetic dipole model. In the

numerical calculation method of magnetic leakage ﬁeld, the ﬁnite element method is

used most widely. Lord and Hwang ﬁrst introduced the ﬁnite element method to the

calculation of the magnetic leakage ﬁeld in 1975. They studied the effects of different

shapes, different dip angles, and the depth and width of crack on the magnetic

leakage ﬁeld. It was pointed out that the numerical calculation was the only feasible

method for solving the problem of magnetic leakage ﬁeld in the nonlinear and

complex shape defects [6]. The results of Lord and Hwang showed that the peak–

valley values of the magnetic leakage ﬁeld were approximately linear proportional to

the increase of the depth of the defect. In 1986, the researches of Hwang and Lord

were tested by Foster, and the results of Lord and Hwang were modiﬁed [7]. In

1980s and 1990s, Atherton [8, 9] and Bruder [10] et al. did a lot of work in the

numerical calcul ation of the magnetic leakage ﬁeld. Atherton calculated the defects

of the pipe wall and obtained a two-dimensional distrib ution model of the magnetic

leakage ﬁeld. Altschuler Eduardo proposed the detection model of nonlinear crack

defect in steel pipe in 1995. He concluded that the induction intensity of the mag-

netic leakage was approximately linear with the increase of the crack depth [11].

In view of the characteristics of the inverse problem of magnetic ﬂux leakage

detection, the existing methods can be classiﬁed as follows:

The direct metho d is to obtain the solution of the inverse problem by solving the

Green equation. However, it is difﬁcult to solve the Green equation. Because of the

solving difﬁculty in direct method, the indirect method to solve the defect param-

eters is proposed. These methods can be divided into three categories: mapping

method, iterative method, and signal classiﬁcation method (Fig. 6.2).

Fig. 6.1 Magnetic dipole

model

186 6 Magnetic Flux Leakage Testing

At present, the theory and implem entation techniques of the simulation matching

algorithm based on statistical methods have been more matured. However, the

statistical method does not have the ability of adaptive processing, and it requires a

large amount of test or simulation data. The statistical process is more complex. The

paper [12] used neural netw ork to calculate the magnetic leakage ﬁeld, and the

nonlinear approximation was used to establish the network model, and the learning

algorithm was given. The drawback of the mapping method is that it relies on the

consistency and accuracy of statistical samples or training samples seriously, and it

is difﬁcult to extend the ability to quantify the actual defects.

The iterative method is widely used in solving the inverse problem of electro-

magnetic ﬁeld [13]. The essence of this method is to solve the inverse problem by

feedback in the way o f solving the positive problem. However, it is time-consuming

for iterative calculati on. Dr. Ramuhalli gave a two-dimensional ﬁnite element

neural network to strike a balance between efﬁciency and accuracy [14]. Dr. Cui

developed it to a three-dimensional ﬁnite element neural network and made it more

available [15].

6.2 Magnetic Flux Leakage Testing Principle

The principle of magnetic ﬂux leakage testing is shown in Fig. 6.3.

Magnetic ﬂux leakage testing method is based on the high-permeability char-

acteristics of ferromagnetic materials. When ferromagnetic materials are magne-

tizing by the external magnetic ﬁeld, if the ferromagnetic material is continuous,

Direct method

Indirect method

Solving integral

equation

Numerical

method

Mapping

method

Iterative method

Signal classification method

Statistical

methods

Neural

network

Numerical model Anal

tical model

Based on

feature

Signal processing

Fig. 6.2 Classiﬁcation of defect quantiﬁcation method

6.1 Introduction 187

uniform, the magnetic ﬁeld will b e constrained in the interior of the materials

mostly. When there are defects in the material, due to the small permeability of the

defect, large magnetic resistance, the magnetic lines will change way. Part of the

magnetic ﬂux from the defect will diffuse and form magnetic ﬂux leakag e above the

surface of the workpiece.

Here, magnetic ﬁeld strength of ferromagnetic material determines the strength

of the magnetic ﬂux leakage of defects directly. Under external magnetizing ﬁeld,

the relationship between the magnetic induct ion intensity

B and the magnetizing

ﬁeld strength

H of ferromagnetic materials is given as:

B ¼ l

H ð6:2Þ

Since the permeability of the material changes with the magnetizing ﬁeld

intensity

H, the relationship between

B and

H is also not linear, and the magne-

tization curve is nonlinear.

The phenomenon of magnetic leakage ﬁeld is demonstrated by an example of the

surface defect in a steel plate. Figure 6.4 is a section of the steel plate, and the

magnetic properties of the steel plate are shown in Fig. 6.5.

The section area of the defect is S

The section area of the steel plate is S. So the

remaining section of the defect area is S − S

. If the magnetizing ﬁeld H is uniform,

the magnetic induction strength without defects is B

. So the working point on the

B-H curve was Q, and the corresponding permeability on curve one is point P.

NSNS

Fig. 6.3 The principle of magnetic ﬂux leakage testing

Defect

Steel plate

Section of the defec

Fig. 6.4 The sketch map of

steel plate with a defect

188 6 Magnetic Flux Leakage Testing

Due to the existence of defects, the magnetic induction intensity in the remaining

section increases, so the working point moves from Q to Q

in the magnetization

curve. However, the corresponding permeability on Q

point changes smaller with

the changing of working point from P to P′ on the curve two. That is to say, due to

the existence of defects, the magne tic induction strength increases on the reduced

cross section, and the permeability of defects is smaller, so a part of magnetic ﬂux

will leak into the surrounding to form defect magnetic ﬂux leakage ﬁeld.

6.3 The Inﬂuence Factors of Magnetic Flux

Leakage Testing

Magnetic leakage ﬁelds of defects will be affected by many factors; these factors

include: the magnetizing magnitude, remanence, electrical conductivity, magnetic

permeability, magnetic coupling loop, the distance between the magnetic poles, the

moving speed of the detector, internal stress, and lift off of the probe.

When the tested material is magnetized, the magnetic leakage ﬁeld can be

generated at the defect, which depends on the magnetizing amplitude. If the

magnetization is not enough, then the remaining thickness of the material is still

possible to carry all the magnetic ﬂux. So no magnetic ﬂux leakage to the surface of

the material can be measured. The tested material should be magnetized nearly

saturated.

Fig. 6.5 The magnetic

properties of the steel plate

6.2 Magnetic Flux Leakage Testing Principle 189

The applied magnetic ﬁeld strength will affect the detection and quantiﬁcation,

so the inﬂuence of the e xternal magnetic ﬁ eld strength will also affect the detection

and quantiﬁcation. The main factors affecting the detection and quantiﬁcation are

the following [16–18].

6.3.1 The Thickness of Material

The greater the thickness of the material is, the stronger the external magne tic ﬁeld

is required to reach saturation magnetization. In the case of constant external

magnetic ﬁeld, the change of the thickness is proportional to the magnetic ﬁeld

intensity and the magnetic induction intensity.

6.3.2 The Component of Material

Because of the change of carbon content, alloy component, and impurities, the

magnetic permeability of the material is changed, and the magnetization of the

material is affected. By using a strong external magnetic ﬁeld, the inﬂuence can be

eliminated by saturation magnetization. At this time, the change of the magnetic

permeability will lead to inconsistence of the leakage magnetic signal. So it is

difﬁcult to effectively evaluate and analyze the testing signal.

6.3.3 The Coupling Loop

In a magnetizing system, steel brushes are used to couple the magnetic ﬂux to the

measured material. The coupling efﬁciency between the magnetizor and the mea-

sured material will have a certain effect on the magnetic induction intensity in the

material. Sh ort steel brush can provide higher coupling efﬁciency and higher

magnetic induction strength, but longer steel brush can improve the pass-through

ability of the inner inspector of pipes. If the applied magnetic ﬁeld strength is only

slightly higher than the saturation level, then the reducing coupling efﬁciency may

decrease the magnetization of the material under saturation.

6.3.4 The Space Between Magnetic Poles

The shorter distance between the magnetizing poles can produce a higher magne-

tization, but this will lead to a decrease in the uniformity of the magnetic ﬁeld.

190 6 Magnetic Flux Leakage Testing

A longer distance between the poles can provide a relativel y uniform magnetic

ﬁeld, but it will reduce the magne tization effect because the magnetic reluctance

between the tested material will increase with the increase of the magnetic pole

spacing, so stronger magnets are needed to make the material to reach saturation.

Therefore, it is necessary to select the appropriate magnetic pole spacing aiming at

the properties and the thickness of the material.

6.3.5 The Speed of Inspector

Because the tested material is a magnetic and electrical conductor, the normal

component of the magnetizing ﬁeld in detector will generate eddy current in the

tested material and thus form a reverse magnetic ﬁeld when the inspector scans. The

eddy current will hinder the magnetic ﬂux to penetrate into the tested material and

induce the change of the magnetic ﬁeld distribution. Through the ﬁnite element

analysis, the inﬂuence of the inspector speed on the axial magnetic induction in the

pipe wall is shown in Fig. 6.6.

In the static case, the axial component of the magnetic induction intensity

of the pipe wall is symmetrically distributed between the two poles. The amplitude

of the magnetic induction intensity decreased by about 10 % when the speed of the

detector was 2 m/s. Therefore, in the design of the magnetizor, it is also necessary

to take into account the actual scanning speed of the detector to ensure that the

magnetic induction intensity of the material can be reached saturation at the design

speed of the detector.

Detector forward direction

Magnet

Pipe

wall

Fig. 6.6 The inﬂuence of the

inspector speed on the axial

magnetic induction in the pipe

wall

6.3 The Inﬂuence Factors of Magnetic Flux Leakage Testing 191

Magnetic leakage signal is a one-dimensional time series, so it can be recon-

structed by using one-dimensional Fourier transformation, and then the effect of

speed is eliminated. By comparing the same defect waveform of magnetic leakage

ﬁeld in static case with the one in dynamic case, a speed compensation ﬁlter model

can be built, as shown in Fig. 6.7.

Figure 6.7a represents the magnetic leakage signal waveform of a stationary

magnetizing ﬁeld. Figure 6.7b represents the magnetic leakage signal wave form

under a constant scanning speed. The approximate expression is a trapezoid. The

gradient ﬁlter is constructed by using the freque ncy domain identiﬁcation method in

system identiﬁcation.

Hð xÞ¼

XðxÞ

SðxÞ

a þ b



a þ b

2xT

þ j

a  b

cosðxTÞð6:3Þ

Among them, HðxÞ is the ratio of the Fourier transformation of the function XðtÞ

and SðtÞ. a and b are the functions of the speed.

The method to determine a

and b

is given below:

• calculate the Fourier transformations of magnetic leakage ﬁeld signals under

velocity V

and stationary state

• obtain the transfer function HðxÞ by (6.3)

• determine a

and b

under the speed by HðxÞ and (6.3)

• least squares ﬁtting the transfer functions of the testing data and the assumed

model data, let the sum of squared errors the least .

6.3.6 The Remanence

Remanence refers to the residual magnetic ﬁeld in the material which has been

tested by magnetic ﬂux leakage detection in the past. The remanence will affect the

current level of magnetization, especially when the magnetizing level is low or

moderate.

The remanence will reduce the magnetic induction intensity of the material being

tested, thus affecting the detection and quantiﬁcation of defects. Ferromaterial in

V>0

S(t)

X(t)

V=0

2T 2T

(a) (b)

Fig. 6.7 A speed compensation ﬁlter model. a The speed is 0; b the speed is more than 0

192 6 Magnetic Flux Leakage Testing

magnetizing will show a hysteresis effect. That is, after the magnetic ﬁeld is

removed, the material will remain within a certain magnetic induction intensity.

When the material is magnetized again, the magnetization process will start from

the remanence; thus, a new magnetization curve is produced. The magnetization

curve is not only nonlinear, but also different from the magnetization each time.

6.3.7 The Internal Stress

The internal stress of materials will affect its magnetic conductivity and magnetic

induction intensity of the materials and defects. The magnetic ﬁeld distribution will

distort and the testing results will be seriously affected. Permanent or plastic

deformation of the material can change the permeability and also affect magne tic

ﬂux leakage testing.

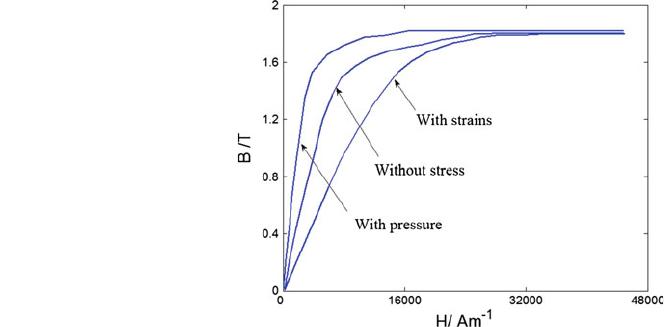
At the lower magnetizing level, the inﬂuence of stress on the magnetic induction

intensity of the material is very serious, as shown in Fig. 6.8. If the mat erial is

magnetized to saturation, the variation of stress can be ignored.

This conclusion should be used for the detection of corrosion. The high level of

magnetization should be used, so that the magnetization of the material can reach a

moderate level of saturation, so as to effectively reduce the inﬂuence of material

component change, the magnetic pole spacing, the detection speed, and the internal

stress on the magnetization and magnetic ﬂux leakage.

6.3.8 The Lift off of Probe

When the probe is scanning on the surface of the material, the surface roughness of

the material, such as the weld seams, defects, will cause the change of the lift off of

Fig. 6.8 The inﬂuence of

stress on the magnetic

induction intensity

6.3 The Inﬂuence Factors of Magnetic Flux Leakage Testing 193

probes. Changes of lift off of the probe induce ﬂuctuations of output signal. It can

be seen as an interference signal and it will adversely affect the results of the testing,

so it should be suppressed.

In order to study the lift off effect of the probe on the magnetic ﬂux leakage

testing for corrosion defects, a typical corrosion defect was simulated. Figure 6.9

shows the relationship between the value of the lift off and the peak – valley value

zp-p

of the magnetic ﬂux leakage.

From Fig. 6.9, the peak– valley value of magnetic ﬂux leakage decreases rapidly

with the increase of the lift off value of the probe. Therefore, in order to improve the

detection sensitivity, the value should be small. However, if the detection sensitivity

of the probe meets the requireme nt of need, the selection of the lift off value should

be to minimize the detection error.

In the case of the above model, the simulation results that the average error is

caused by the probe ﬂuctuation of 0.5 mm are shown in Fig. 6.10.

Fig. 6.9 The relationship

between the value of the lift

off and the peak–valley value

zp-p

of the magnetic ﬂux

leakage

Fig. 6.10 The errors caused

by the probe ﬂuctuation of

0.5 mm

194 6 Magnetic Flux Leakage Testing