Modeling the Ductile-Brittle Transition Behavior

in Thermomechanically Controlled Rolled Steels

S.J. WU, C.L. DAVIS, A. SHTERENLIKHT, and I.C. HOWARD

The Charpy impact transition temperature (ITT) is well modeled for hot-rolled or normalized steels

having uniform grain size using empirical equations. However, the ITT of nonhomogeneous steel

microstructures, such as duplex (mixed fine and coarse) grain sizes, and the scatter in experimental

Charpy energy values, observed in the transition region, are not accurately modeled. This article

describes research on the microstructure-fracture property relationship and the prediction of the ITT

using a cellular automata finite element (CAFE) model in thermomechanically controlled rolled

(TMCR) Nb-microalloyed steels. The ferrite grain size distributions for two TMCR steel plates were

analyzed and used for the prediction of the local fracture stress (



) values based upon the Griffith

model. It was found that the coarse grain size distribution could be used to predict the range of



values observed. The CAFE model was used to predict the ITT using the predicted



distribution

for a TMCR steel. Results showed that the CAFE model realistically predicted the Charpy ITT; in

particular, it was able to reproduce the scatter in values in the transition region. Within the model,

the percentage of brittle failure and the upper shelf ductile energy were predicted well. However, the

lower shelf brittle energy was overestimated due to computational limitations in the commercial FE

software used with the current CAFE model.

I. INTRODUCTION

ESPITE

many advances made in (sharp crack) frac-

ture toughness testing and assessment procedures over the

last 30 years, the vast majority of steel products are released

to a specification that is based on energy absorption in the

Charpy notched bar impact test (defined in ASTM Stan-

dard E 23), carried out at a prescribed low temperature.

Body-centered cubic metals, such as mild steels, demon-

strate a transition from a ductile fracture mode to a brittle

cleavage failure mechanism as the test temperature

decreases. The ductile-brittle transition may occur over a

temperature range of only a few degrees Celsius, or a wide

range of over 100 degrees, depending upon the microstruc-

ture and specimen geometry (thereby the applied stress-

strain states in the specimen). Extensive studies have been

carried out, over the past 40 years, to determine the quan-

titative structure-property relationships in steels. As a result,

many empirical equations have been proposed to relate the

strength and impact behavior to the microstructure and com-

position of the steels.

[1–4]

It is well established for hot-rolled

or normalized ferrite-pearlite microstructures that the yield

strength (



[5,6]

the critical local fracture stress (



[7]

and

the Charpy impact transition temperature (ITT)

[8]

are a lin-

ear function of , where is the mean grain size of

polygonal ferrite.

The empirical equations, however, can only be applied to

materials regarded as “uniform, homogeneous,” such as nor-

malized steels, which have a single size distribution of fer-

rite grains together with small and finely distributed carbides,

thereby allowing an average grain size to be used for pre-

diction. The fracture properties of such materials are essen-

tially single-valued functions within random experimental

errors and can be expressed using average microstructural

parameters such as mean grain size. Whereas for nonho-

mogeneous materials, such as steels with a duplex ferrite

grain structure, seen in many thermomechanically control

rolled (TMCR) steels, the average grain size parameter does

not properly represent the microstructure,

[9]

and therefore

cannot be used to predict the cleavage fracture stress and

ITT. It has been reported that cleavage microcracks form

preferentially in the largest polygonal ferrite grains,

[10]

sug-

gesting that the



value should correlate with some mea-

sure of the large grains rather than the mean value of the

grain size distribution.

[10–13]

Previous experimental results

[14]

have shown that there can be a large scatter in



value for

TMCR steels, and a mean



value has little meaning in

describing the fracture behavior. The distribution of the



values is therefore required to describe the fracture behav-

ior of these nonhomogeneous steels.

In other words, in order to predict the ITT for nonhomo-

geneous steels, such as TMCR steels, one has to simulate

the brittle fracture behavior of a material as that of an ensem-

ble of grains of different sizes, i.e., with different fracture

stresses. The TMCR steels are produced as steel plate, pipe,

tube, and sections for the construction, oil, and gas indus-

tries, among others. Release specifications are still based on

Charpy-notched bar impact test results. Consequently, the

ability to model the ITT behavior is advantageous when

developing new TMCR steels/processing routes and opti-

mizing performance in existing grades.

(d )

1/2

METALLURGICAL AND MATERIALS TRANSACTIONS A VOLUME 36A, APRIL 2005—989

S.J. WU, formerly Research Fellow, Department of Metallurgy and

Materials, The University of Birmingham, is Assistant Professor, School

of Materials Science and Engineering, Beijing University of Aeronautics

and Astronautics, Beijing 100083, P.R. China. C.L. DAVIS, Senior Lec-

turer, is with the Department of Metallurgy and Materials, The University

of Birmingham, Birmingham B15 2TT, United Kingdom. Contact e-mail:

[email protected] A. SHTERENLIKHT, formerly Research Student,

Department of Mechanical Engineering, The University of Sheffield, is

Research Fellow, Materials Science Centre, University of Manchester,

Manchester, M1 7HS, United Kingdom. I.C. HOWARD, Professor, is with

the Department of Mechanical Engineering, The University of Sheffield,

Sheffield S1 3JD, United Kingdom.

Manuscript submitted May 6, 2004.

990—VOLUME 36A, APRIL 2005 METALLURGICAL AND MATERIALS TRANSACTIONS A

Modeling of the ductile-to-brittle transition behavior in

steels is usually performed with the “local approach” to frac-

ture.

[15–21]

In this approach, micromechanical models for

fracture are constructed in which the failure criteria are based

on stress, strain, and damage levels local to the crack tip.

The most widely used model for the local approach to cleav-

age is that of Beremin.

[22]

In this model, the probability of cleavage P is calculated

[1]

where



is the Weibull stress, which is a function of the

maximum principal stresses in the plastic zone,



is the ref-

erence stress, and m is the Weibull modulus. The reference

stress is calculated as the Weibull stress for plane strain

small scale yielding conditions. The shape parameter con-

trols the shape of the Weibull distribution function, and



and m are considered to be true material properties, inde-

pendent of geometry and loading mode, which are calibrated

by FE modeling of the appropriate experimental results at

the lower shelf temperatures.

[16]

In FE discretization,



is defined as

[2]

where



is the maximum principal stress in the ith FE, V

volume of the ith element, and V

is a characteristic volume

of material.

By using the distribution for m rather than a single value,

it is thus possible to simulate the fracture stress distributions

within the classical local approach framework. Indeed, if the

ith FE is given a randomly generated m

, then the Weibull

stress from Eq. [2] can be rewritten as

[3]

where m* denotes the mean value across the FEs in the plas-

tic zone.

Thus, FEs with higher m

will contribute more to the

Weibull stress and to the probability of cleavage than those

with lower m

. It is therefore logical to relate FEs with higher

to lower fracture stress and those with lower m

to high

fracture stress. The local approach model for cleavage based

on the Weibull stress calculated according to Eq. [3] is thus

capable of simulating brittle fracture behavior of a material

composed of grains of different sizes. However, the added

level of detail means that the number of calibration simu-

lations have to be increased by an order of magnitude. Indeed,

simulations with different parameters for the distribution of

m will yield different results, and also the outcome of each

run with m values generated from a given distribution will

be different. This is because the shape parameter of the

Weibull distribution, m, now has a distribution assigned to

it. Assigning distributions to parameters is at the core of the

Bayesian statistics, whereas classical statistics treats param-

eters as constant.

A number of local models for ductile damage exist, of

which the most widely used are the Gurson

[23,24]

model and

that of Rousselier et al.

[25,26]

The cellular automata finite ele-

ment (CAFE) model reported here uses the Rousselier model

to represent the development of ductile damage, principally

 {

)

}

1/m*



{



)

}

1>m

P  1  exp (s

)

because of its combination of simplicity and realism. How-

ever, comparable results could be obtained by encoding the

Tvergaard-modified

[24]

Gurson

[23]

model.

Although the local approach model described previously

has some potential, it suffers from two well-known problems

of pure FE modeling of the transitional ductile brittle frac-

ture. The first problem is that the microstructurally signifi-

cant size scales are very different for the ductile and the brittle

fracture mechanisms. Therefore, it is hard to relate the FE

size to both the ductile and the brittle size scales.

[15–17,27]

The

second problem is that the size of the FE mesh in the dam-

age zone is very small, typically 0.05 to 0.5 mm. Thus, many

FEs are required to mesh even a small sized sample (e.g., a

Charpy specimen). The computation of such a model becomes

a challenge in itself.

In this work, a recently developed CAFE model for frac-

ture

[27–30]

was used instead of the pure FE local approach

analysis. In this model, the structural and material parts of

the simulation are separated into two entities. The struc-

tural changes in the model geometry are simulated with the

FEs, the sizes of which are chosen only to adequately rep-

resent the macrostrain gradients. All material information

is stored and processed in an appropriate number of cellu-

lar automata arrays (CA arrays). This model is fast com-

pared to the pure FE approach because significantly larger

FEs can be used; thus, the total number of FEs is much

smaller. Moreover, different size scales relevant to the duc-

tile and the brittle fracture mechanisms can be easily

employed by using two CA arrays with cells of different

size. The CAFE model is described in greater detail else-

where.

[27–30]

Some details of particular importance for the

present work are given in Section II.

The present article examines the relationship between the

critical local fracture stress and the coarse ferrite grains for

two TMCR steels and, using the relationship as input to the

CAFE model, attempts to predict their ductile-brittle tran-

sition behavior.

II. EXPERIMENTAL

Two microalloyed TMCR steel plates (plates 1 and 2)

were used in this work. The nominal chemical compositions

of the steel plates are listed in Table I. The original/final

gages of the plates are 230 mm/40 mm for plate 1 and

230 mm/50 mm for plate 2. Full details of the TMCR pro-

cessing schedule are given elsewhere.

[31]

The steel plates were characterized on all three planes

(plate 1 shown in Reference 31), with the section normal to

the transverse direction (TD) being quantified. Both plates

showed very similar microstructures. Statistical analyses of

the ferrite grain size distributions were carried out, using

optical microscopy and image analysis software (ZEISS

KS400 3.0), on a minimum of 1200 grains on samples

ground, polished, and etched with 2 pct Nital. The grain size

is represented by the equivalent circular diameter (ECD)

converted from the grain area.

Blunt-notch four-point-bend specimens were chosen to

determine the local fracture stress



. The dimensions of

the blunt-notch bend specimens were 10  10  60 mm

with a 45 deg notch of 3.3-mm depth and 0.2-mm root

radius. The notches were cut along the section normal to

METALLURGICAL AND MATERIALS TRANSACTIONS A VOLUME 36A, APRIL 2005—991

the TD. The blunt-notch tests were carried out between

160 °C and 196 °C using a 50-kN DMG tensile testing

machine with a loading rate of 0.5 mm/min. The stress-

strain distribution ahead of the notch root has been analyzed

using the FE method

[32]

together with appropriate values

of yield strength and strain-hardening rate of the steels. The

distance between the two inner loading points (S

min

) was

20 mm, and the span between the two outer loading points

max

) was 50 mm. The testing temperature was controlled

using a low-temperature bath, insulated from the actuator

of the testing machine. The specimen was put in the bath

on two steel rollers (separation 50 mm), applying a 2-kN

steady load to the specimen. Liquid nitrogen was used to

cool the bath, the specimen, and the fixture crosshead to the

required temperature, holding for over 30 minutes, before

starting the test. The temperature was measured using a

thermocouple inserted into the 4- to 5-mm-deep hole at one

Table I. Nominal Chemical Compositions (Wt Pct) of the Steel Plates Used

Plate C Si Mn P S Cr Ni Al Cu Nb N Ti V

1 0.11 0.31 1.39 0.010 0.003 0.03 0.32 0.037 0.033 0.024 0.006 0.002 0.045

2 0.11 0.30 1.43 0.011 0.003 0.023 0.30 0.039 0.013 0.040 0.005 0.003 0.063

(a)

(b)

Fig. 1—FE model of the Charpy test (a) before and (b) at the end of the simulation.

end of the specimen. Liquid nitrogen was added to the bath,

as required to keep the temperature within 2 °C during

the test.

The model of the Charpy test consisted of the sample, the

anvils, and the tup (Figure 1(a)). Of these, only the damage

zone of the Charpy sample was modeled with the CAFE

approach; the rest were simulated with pure FE. The dam-

age zone, i.e., the area where the fracture might take place,

was defined as 10  10  10  1000 FE cubes located in

the center of the sample to accommodate any crack propa-

gation path. Figure 1(b) shows all modeled bodies at the end

of the simulation. The sample fractures completely except

for a 1-FE-long remaining ligament, which underwent large

plastic shear deformation (plastic collapse). The failed FEs

are removed from the mesh and are not shown. For the

purpose of the present work, the CAFE model was con-

structed as shown in Figure 2.

[22]

Each FE has two CA arrays

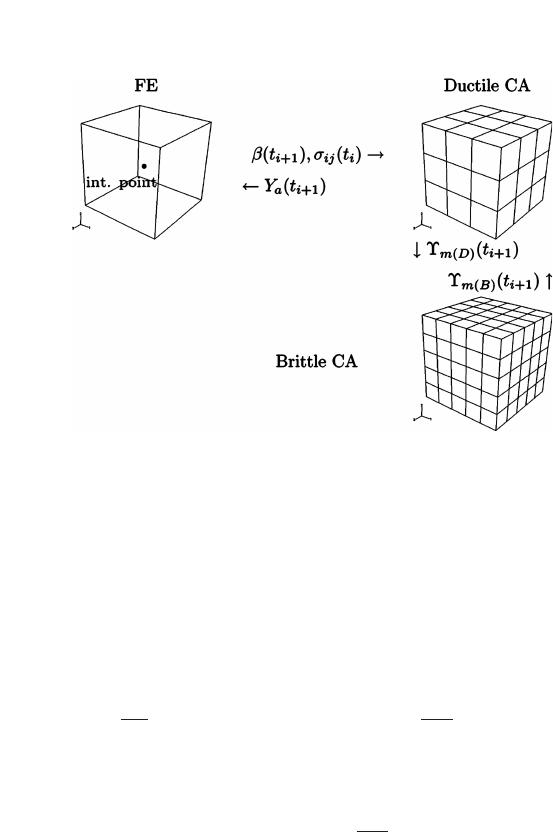
992—VOLUME 36A, APRIL 2005 METALLURGICAL AND MATERIALS TRANSACTIONS A

attached to it, one representing the ductile properties of the

steel (the ductile CA array) and the other addressing the

brittle properties of the material (the brittle CA array). The

Rousselier ductile damage model

[25,26]

was used as a con-

stitutive routine at each FE integration point. The plastic

potential in this model has the form

[4]

where



and



are internal variables:

[5]

[6]

where



 a scalar damage variable,



 a dimensionless density,

D and



 material constants, which must be tuned,

 the initial void volume fraction, and

H(

)  the hardening term.

The dot on top of a symbol denotes a time derivative.

Each ductile CA cell is given a randomly generated crit-

ical value of the damage variable,



, at the beginning of

the simulation. The current value of the damage variable,



i1

), calculated at the integration point, is sent to the duc-

tile CA array and distributed across all cells according to

local strain gradients associated with dead cells.

A dead ductile cell simulates a microvoid, which is a

source of local strain concentration. In this CAFE model,

such strain concentration is implemented by using the duc-

tile strain concentration factor, c

, in those cells adjacent

to a dead one, which lie on the plane perpendicular to the

direction of the maximum principal stress. Accordingly,

the brittle strain concentration factor, c

, is utilized in the

brittle CA array for the same purpose. In the present model,

both concentration factors were kept constant and indepen-

dent of the shape or size of a crack or a microvoid.

r  1/(1  f

 f

exp b)

 

D exp a

 H(

)  Ds

r exp b exp a

b  0

The ductile failure criterion at each ductile CA cell is

based on the damage variable exceeding the critical value

given to this cell. Thus, a ductile cell will become inactive

at time increment n if the damage parameter



) exceeds

its critical value



. Each brittle cell is given a randomly

generated grain size, d, from within a given distribution, and

an orientation angle,



, at the beginning of the simulation.

Moreover, it is assumed that a constant fraction of brittle

cells (in this case, 0.005) have microcracks from the very

beginning of the simulation. Only these cells can initiate

brittle fracture propagation.

The maximum principal stress at the FE integration point

is redistributed across the brittle CA array. A brittle CA cell

is considered to have failed if the maximum principal stress

in this cell exceeds the fracture stress for the grain size

assigned to this cell. Brittle fracture will propagate from

one cell, k, to another, l, only if the misorientation angle

for these cells is smaller than the misorientation threshold,

i.e., if |







| 



. It is further assumed that the misori-

entation threshold is temperature sensitive:



 0 at tem-

peratures above 20 °C; from 20 °C to 80 °C,



linearly increasing to 60 deg; and



 60 deg at tempera-

tures below 80 °C. We have found that a constant, tem-

perature-independent misorientation threshold leads to a very

poor prediction of the experimental ductile-brittle transi-

tion curve. It was thus assumed that the misorientation thresh-

old might be temperature dependent and this dependence

was chosen to achieve a better prediction of the transition

curve. Such an approach is similar to that of Burstow,

[16]

who concluded that the Beremin model can correctly predict

the temperature dependence of the cleavage probability if

the parameters of the Beremin model, m and



, are tem-

perature dependent. The values for these parameters for each

experimental temperature were tuned using the toughness

scaling technique.

[16]

Such temperature dependence of



promotes fast brittle fracture propagation at the lower shelf

temperatures and inhibits or stops it at the upper shelf. The

changes in cell state in one CA array, either brittle, Y

m(B)

 1), or ductile, Y

m(D)

 1), cause some change of the

cell states in the other CA array (Figure 1).

Finally, the state variables of the FE, Y, are calculated

and returned back from the CA part of the model to the FE

solver. There are two state variables in this model: the

integrity of the FE, Y

, and the percentage of the brittle

phase per FE, Y

. At the beginning of the simulation,

)  1, which means that there is no damage. Accord-

ingly, Y

)  0 means that either the FE has no load-

bearing capacity or that the crack has propagated across

the entire of the FE by time increment n. With each new

dead cell, Y

decreases. As there are many cells per FE,

the transition from Y

 1 to Y

 0 is smooth.

This work was aimed at the ITT prediction of the Charpy

impact test for TMCR steels. A three-dimensional FE model

of the Charpy test was created in which 900 FEs located at

and near the macroscopic fracture propagation plane (dam-

age zone) were simulated with the CAFE approach.

[22]

The

5  5  5 cell ductile and 10  10  10 cell brittle CA

arrays were created for each FE in the damage zone. Thus,

the ductile damage cell size was 0.2 mm and the brittle dam-

age cell size was 0.1 mm (it should be noted that the shape

of the CA array is not linked to the shape of the FE mesh

and remains the same throughout the simulation).

Fig. 2—Representation of the CA arrays for ductile and brittle failure asso-

ciated with each FE cell in the CAFE model.

METALLURGICAL AND MATERIALS TRANSACTIONS A VOLUME 36A, APRIL 2005—993

Fig. 3—Microstructure of the TMCR microalloyed steel showing coarse and

fine grain sizes.

Fig. 4—Equivalent circle diameter ferrite grain size distributions for the

large (6



m) grains located within the coarse grain bands of the two

TMCR microalloyed steels.

III. RESULTS AND DISCUSSION

A. Microstructural Characterization

The two TMCR steel plates have very similar microstruc-

tures comprised of ferrite/pearlite banded in the rolling direc-

tion (Figure 3). The pearlitic bands are approximately 10



wide and are similar in the two steel plates. Variations in

ferrite grain sizes were frequently observed through the thick-

ness with coarse ferrite grain patches studded in a matrix

of desirable fine grains resulting in a “duplex” ferrite grain

distribution. The duplex grain structure may stem from a

nonhomogeneous distribution of microalloying element pre-

cipitates,

[9]

especially niobium.

[33,34]

Segregation of niobium

and other alloying elements during solidification results in

a nonhomogeneous distribution of microalloying precipitates

and consequently partial recrystallization can occur during

the TMCR process.

As reported in the literature,

[10,11]

for steels having a

bimodal distribution of polygonal ferrite grains (comprising

bands of coarse and fine grains), cleavage microcracks form

preferentially in the largest grains. A cleavage microcrack

formed in a large grain within a coarse grain patch or band

will propagate through the large grains within the band and

may carry on to cause catastrophic cleavage failure if the

stress intensification resulting from the cleavage crack in

the coarse grains exceeds the fracture strength of the sur-

rounding fine ferrite grains. The large grains in the coarse

grain patches are therefore regarded as the “weak link” and

the dominant microstructural factor in the cleavage fracture

process. In this work, the ferrite grains within the coarse

grain patches were analyzed for the two TMCR steels by

setting a lower ECD grain size threshold limit of 6



during quantification. The grain size distributions from

through-thickness characterization are shown in Figure 4.

The mean coarse grain size of 12.2



m for plate 1 is smaller

than that for plate 2 (13.2



m). The average areal propor-

tions of the coarse grain patches are 38.7 and 47.1 pct for

plates 1 and 2, respectively. Therefore, there is a signifi-

cant statistical chance of a crack tip sampling a coarse grain

patch. The small grain size for plate 1 is 4.8



m and for

plate 2 is 5.2



B. Critical Local Fracture Stress (



)

Critical local fracture stress (



) values for both TMCR

steels were determined using values of fracture load in com-

bination with a two-dimensional FE analysis of the stress-

strain distribution ahead of the notch root under plane strain

conditions.

[32]

The stress-strain distributions were expressed

in terms of the ratio of maximum principal stress to yield

strength,



, corresponding to the position ahead of the

notch tip and the largest value of



at each applied load

normalized by the general yield load (P

app

). Assuming

that the largest maximum principal stress corresponding to

the failure load of the specimen is the critical local fracture

stress



, the



values for the two TMCR steels can then

be obtained from the failure loads of the blunt-notch four-

point-bend specimens and the yield stress values determined

through tensile tests at different temperatures. Fractogra-

phy revealed that no inclusion-initiated failure was observed.

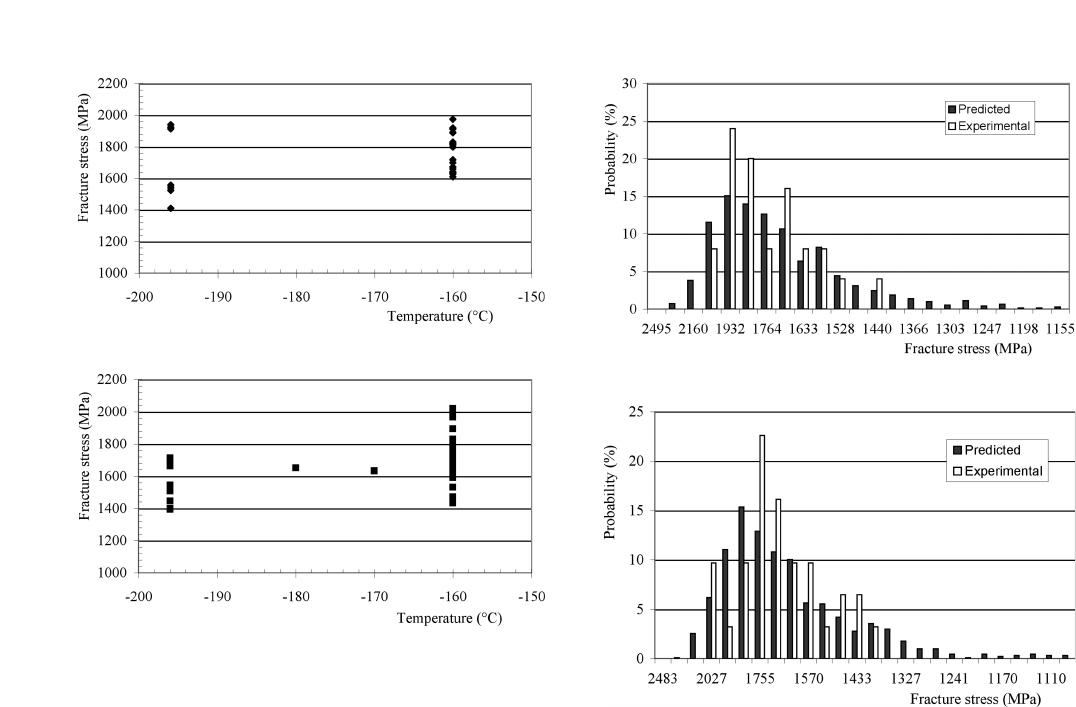
Figure 5 shows the experimentally determined



values

for the two steels tested at different temperatures. It can be

seen that the



values are almost independent of tempera-

ture and that a large scatter in



values exists for both steels

due to the duplexity of the ferrite grain sizes. The mean



value of 1749 MPa for plate 1 is greater than that of plate

2 (1666 MPa). This is probably due to the consistently

smaller grain size (overall size, 7.1



m in plate 1 and 8.2



in plate 2, and coarse size) and the smaller area fraction of

the coarse grain bands in plate 1.

C. Prediction of



from Grain Size Distribution

Significant scatter in the



values (Figure 5) is revealed

by a very limited number of tested specimens. It can be pos-

tulated that the scatter will be smaller with more specimens

tested. A great number of specimens are required to thor-

oughly describe the real



distribution that is a crucial input

to the CAFE model for the prediction of the ductile-brittle

transition temperature. Since experimental tests are time and

money intensive, attempts were made to predict the



dis-

tribution from the microstructure of the steels.

The well-established empirical expressions for normal-

ized steels may still be applicable to predict the tensile

994—VOLUME 36A, APRIL 2005 METALLURGICAL AND MATERIALS TRANSACTIONS A

strengths of the TMCR steels using their mean grain size,

because tensile tests average the microstructure (for ductile

failure) as the strain field samples a relatively large area

compared to the scale of the microstructure. The mean grain

size for the duplex grains, however, cannot be used to pre-

dict the Charpy impact energy and the fracture stress due

to the highly concentrated stress and strain ahead of the

notch or fatigue-precrack tip. Failure of the notched or pre-

cracked specimens is dominated by the intensification of

stress and strain within a small area, usually the plastic zone,

in front of the notch or crack, which strongly limits the sam-

pling of the microstructure. As a result, a large variation in

fracture properties will appear for steels with nonuniform

microstructure. A single-valued function obtained from the

mean grain size is not representative of the fracture prop-

erties such as



and ITT for such steels.

The ferrite grain size distribution must therefore be used

to predict the distribution of the



values. It has been

shown

[7,35]

that the critical event for cleavage failure in a

notched steel specimen is the propagation of a microcrack

across the adjacent ferrite/ferrite grain boundary. This will

occur when the stress level at the microcrack exceeds the

“ferrite grain strength,” which is given in terms of the grain

diameter d by Eq. [7]:

[7]

where E is Young’s modulus,



is Poisson’s ratio, and



the effective surface energy for creation of new crack sur-

faces. Assuming that the mean local fracture stress of the

TMCR steels is related to the mean ferrite grain size of the

 [pEg

/(1  n

)d]

1/2

grains within the coarse grain patches (since cleavage micro-

cracks will form preferentially in the large polygonal ferrite

grains), the



value can then be determined, using Eq. [4]

and



 0.3, E  208  10

MPa. A value of



of 52 J/m

is obtained for both TMCR steels, which is in the range

reported in the literature.

[36]

Using Eq. [7] and the obtained



value, the coarse ferrite grain size distributions in Figure 4

can then be converted into local fracture stress distributions.

The probability of cleavage failure occurring at a certain

fracture stress value calculated from Eq. [7] corresponding to

a particular grain size is shown in Figure 6 together with the

experimental results of the



values. The reason that there

are no experimental test data at the lower value side of the



distributions, on the right-hand side of the graphs, is attrib-

uted to the limited number of tested specimens and the very

low probability of sampling the extremely large ferrite grains

due to their rarity. It can be seen that the experimental results

fit very well to the predicted



distributions obtained from

Eq. [4] based upon the coarse ferrite grain distributions for

the two TMCR steels. This implies that the fracture stress



of a TMCR microalloyed steel can be predicted based on the

coarse grain size distributions within the coarse grain bands.

This fracture stress distribution can then be used as an input

into the predictive CAFE model for ITT.

The ductile part of the CAFE model was tuned using the

Charpy test modeling at the upper shelf temperatures, where

the model does not exhibit any significant brittle fracture.

(a)

(b)

Fig. 6—Comparison of the local fracture stress distribution predicted from

the coarse grain size distribution with the experimental data: (a) plate 1

and (b) plate 2 steel.

(a)

(b)

Fig. 5—Variation of the local fracture stresses with temperature for the

two TMCR steels: (a) plate 1 and (b) plate 2.

METALLURGICAL AND MATERIALS TRANSACTIONS A VOLUME 36A, APRIL 2005—995

(a)

(b)

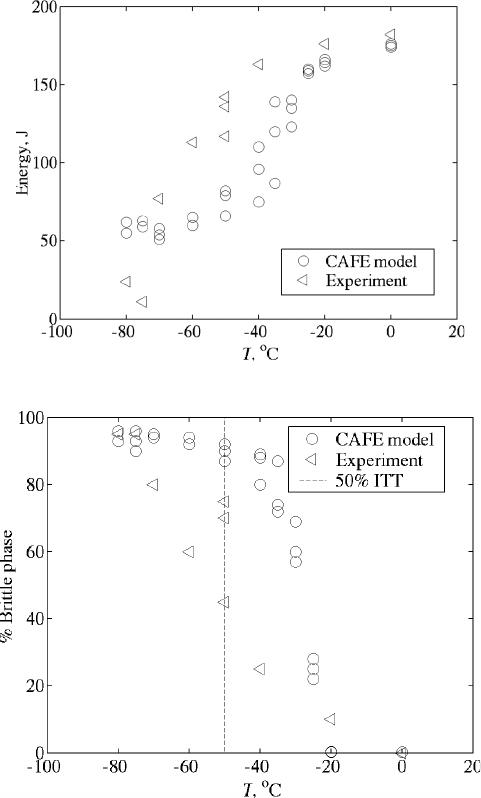
Fig. 7—CAFE model results for (a) total energy absorbed and (b) per-

centage brittle phase vs temperature compared to the experimental results

for TMCR Nb-microalloyed steels.

The strain concentration coefficients were chosen as c



1.4 and c

 11 so that the concentration around a failed

brittle cell (microcrack) is much higher that that around the

dead ductile cell (microvoid).

The experimentally measured grain size distribution for

another TMCR Nb-microalloyed steel (nominal composi-

tion same as plate 2), with known Charpy DBTT curve, was

simulated in the CAFE model using a random number gen-

erator based on a Weibull three-parameter probability den-

sity function. The parameters of this function were chosen

such that the mean, standard deviation, and mode calculated

on the generated values are the same as those calculated

from the experimental grain size data. Each brittle cell was

then assigned a fracture stress calculated with Eq. [7] for a

grain size generated for this cell.

The modeling was performed at 11 temperatures from

80 °C to 0 °C, with three simulations at each temperature.

The resulting total energy absorbed and the percentage of

the brittle phase values are shown in Figures 7(a) and (b)

accordingly. Figure 7(a) indicates that the lower shelf starts

at approximately 50 °C to 60 °C. These temperatures

can be taken as the energy-based ITT. On the other hand,

the 50 pct ITT obtained from the data shown in Figure 7(b)

is approximately 30 °C to 35 °C. Although in general

the model predicts a higher ITT than observed experimen-

tally, the shape of the transition curve is well reproduced.

The scatter in the simulated energy and brittle phase values

is due to the fact that each modeling run represents a unique

sampling of





, and



. Therefore, each simulation has

a unique fracture propagation history.

Figure 7(a) shows that the CAFE model overpredicts

(approximately 60 J) absorbed energies for 100 pct brittle

failure. This is because the present CAFE model cannot sim-

ulate crack propagation from one FE into another due to the

restrictions of the Abaqus code.

[23,26]

Consequently, brittle

fracture has to reinitiate when a crack crosses a FE bound-

ary. In each run, the crack has to cross approximately 100

FEs (the exact number depends on the actual fracture prop-

agation path). As crack initiation requires plastic deforma-

tion, the total absorbed energy becomes high. Further model

development will be to allow crack propagation from one

FE to another.

An important feature of the present CAFE model is that

temperature-dependent scatter in both the energy and the

percentage of brittle phase was achieved. The scatter is

caused by the fact that the locations of the brittle CA cells

representing larger grains vary randomly from one modeling

run to another. It has been argued that in the upper shelf,

the number of larger grains that can fail is so small that

their locations do not matter, as it is extremely unlikely that

one such grain will be found in the crack propagation path.

[27]

Similarly, in the lower shelf, there are so many grains that

can fail that their locations also are not important, as many

such grains will be found along any crack propagation path.

However, at transitional temperatures, the number of larger

grains that can fail is such that their locations become

important as different fracture propagation paths will cross

a larger grain at different crack lengths, or will not cross

any such grain at all. Accordingly, the level of scatter is

higher in the transition region than in the upper and in the

lower shelves.

[37–40]

Such modeling behavior agrees with

the experimental observations (Figure 7) where the

experimental scatter in the transition range can be seen from

the tests at 50 °C. In addition, it is impossible to achieve

this scatter if only the mean grain size (fracture stress) is

used in the model.

In summary, it has been shown that the observed

microstructural inhomogeneity (fine and coarse grain sizes)

translates into a distribution of fracture stress values, which

can be predicted from the coarse grain size distribution. This

fracture stress distribution can be used with a novel model-

ing approach (CAFE model) to reproduce the scatter seen

experimentally in Charpy impact testing and predict the

Charpy ITT behavior.

IV. CONCLUSIONS

A combined experimental and modeling approach to

understanding and predicting the scatter in Charpy

ITTs for thermomechanically controlled rolled (TMCR)

996—VOLUME 36A, APRIL 2005 METALLURGICAL AND MATERIALS TRANSACTIONS A

Nb-microalloyed steels has been carried out. The major find-

ings are as follows.

1. A significant degree of scatter in experimentally determined

fracture stress (



) values exists for the Nb-microalloyed

TMCR steels investigated. The



distribution can be pre-

dicted, with reasonable accuracy, from the coarse grain size

distribution.

2. A CAFE model has been developed using experimental

data (fracture stress distribution) as input. The results

from multiple runs of the model showed that a realistic

prediction of the Charpy ductile-brittle transition behav-

ior could be achieved. In addition, the experimentally

observed scatter in Charpy energy values in the transi-

tion region can also be seen in the model.

3. The CAFE model prediction of the upper shelf ductile

energy and percentage brittle failure for the Charpy impact

test agrees well with the experimental data. The prediction

of the lower shelf brittle energy is not as good due to

computational limitations (Abaqus code) of the current

CAFE model.

ACKNOWLEDGMENTS

The authors thank the Engineering and Physical Sciences

Research Council (EPSRC) for financial support and Corus

UK Ltd. for financial support, provision of test material,

and data.

NOMENCLATURE

, c

strain concentration coefficients for the

ductile and the brittle CA arrays

D parameter of the Rousselier’s model

d grain size

initial void volume fraction in the Rousselier’s

model

H hardening term in the Rousselier’s model

E Young’s modulus

m Weibull modulus

Weibull modulus of the FE i

m* the mean Weibull modulus across all FEs in

the plastic zone

P probability of cleavage

app

applied load

general yield load

time at increment i

volume of ith FE

characteristic volume of material

integrity of a FE

percentage of brittle phase per FE

m(B)

, Y

m(D)

state of cell m in the brittle or the ductile CA

array



damage variable of the Rousselier’s model



critical value of the damage variable



effective surface energy



equivalent plastic strain



Poisson’s ratio



orientation angle of cell l



grain misorientation threshold



dimensionless density



parameter of the Rousselier’s model



local fracture stress



Von Mises equivalent stress



the maximum principal stress



mean stress



reference stress



Weibull stress



yield stress

REFERENCES

1. B. Mintz, G. Peterson, and A. Nassar: Ironmaking and Steelmaking,

1994, vol. 21, pp. 215-22.

2. T. Gladman, D. Dulieu, and I.D. McIvor: Microalloying 75, Union

Carbide Corp., New York, NY, 1977, pp. 32-55.

3. B. Mintz, W. B. Morrison, and A. Jones: Met. Technol., 1979, vol. 6,

pp. 252-60.

4. W.E. Duckworth and J.D. Baird: J. Iron Steel Inst., 1969, vol. 207,

pp. 854-71.

5. E.O. Hall: Proc. Phys. Soc., 1951, B64, pp. 747-53.

6. N.J. Petch: J. Iron Steel Inst., 1953, vol. 173, pp. 25-28.

7. T. Lin, A.G. Evans, and R.O. Ritchie: Metall. Trans. A, 1987, vol. 18A,

pp. 641-51.

8. T. Gladman: The Physical Metallurgy of Microalloyed Steels, The

Institute of Materials, London, 1997, p. 62.

9. C.L. Davis and M. Strangwood: J. Mater. Sci., 2002, vol. 37,

pp. 1083-90.

10. M.T. Shehata and J.D. Boyd: in Advances in Physical Metallurgy and

Applications of Steels, Proc. Conf., TMS, Warrendale, PA, 1982,

pp. 229-36.

11. J.H. Chen, L. Zhu, and H. Ma: Acta Metall. Mater., 1990, vol. 38,

pp. 2527-35.

12. J.H. Chen, G.Z. Wang, Z. Wang, L. Zhu, and Y.Y. Gao: Metall. Trans.

A, 1991, vol. 22A, pp. 2287-96.

13. A. From and R. Sandstrom: Mater. Characterization, 1999, vol. 42,

pp. 111-22.

14. S.J. Wu and C.L. Davis: Paper presented at ICSMA13, Budapest, 2003,

Mater. Sci. Eng. A, in press.

15. I.C. Howard, Z.H. Li, M.A. Sheikh, A.H. Sherry, D.P.G. Lidbury, and

D.W. Beardsmore: IMechE Seminar, ‘20 Years of R6’, IMechE HQ,

London, Nov. 20, 1996.

16. M.C. Burstow: Int. J. Pressure Vessels Piping, 2003, vol. 80,

pp. 797-805.

17. I.C. Howard, Z.H. Li, and M.A. Sheikh: Fatigue and Fracture Mechan-

ics, 30th volume, ASTM STP 1360, P.C. Paris and K.L. Jerina, eds.,

ASTM, West Conshohocken, PA, 2000, pp. 152-68.

18. L. Xia and F.S. Shih: J. Mech. Phys. Solids, 1995, vol. 43, pp. 233-59.

19. C. Ruggieri and R.H. Dodds: Int. J. Fracture, 1996, vol. 79, pp. 309-40.

20. L. Xia and F.S. Shih: J. Mech. Phys. Solids, 1996, vol. 44, pp. 603-39.

21. L. Xia and L. Cheng: Int. J. Fracture, 1997, vol. 87, pp. 289-306.

22. F.M. Beremin: Metall. Trans. A, 1983, vol. 14A, pp. 2277-87.

23. A.L. Gurson: J. Eng. Mater. Technol., 1977, vol. 99, pp. 2-15.

24. V. Tvergaard: Int. J. Fracture Mech., 1981, vol. 17, pp. 389-407.

25. G. Rousselier, J.C. Devaux, G. Mottel, and G. Devesa: in Nonlinear

Fracture Mechanics: Volume II—Elastic Plastic Fracture, J.D. Landes,

A. Saxena, and J.G. Merkle, eds., ASTM STP 995, Philadelphia, PA,

1983, pp. 332-54.

26. G. Rousselier: Nucl. Eng. Design, 1987, vol. 105, pp. 97-111.

27. A. Shterenlikht: Ph.D. Thesis, Sheffield University, 2003.

28. J.H. Beynon, S. Das, I.C. Howard, and A. Chterenlikht: in New and

Emerging Computational Methods: Applications to Fracture, Damage

and Reliability, F.W. Brust, ed., ASME, 2002, pp. 229-37.

29. J.H. Beynon, S. Das, I.C. Howard, E.J. Palmiere, and A. Chterenlikht:

in ECF14, Fracture Mechanics Beyond 2000, A. Neimitz, I.V. Rokach,

D. Kocanda, and K. Golos, eds., EMAS Publications, Sheffield, United

Kingdom, 2002, pp. 241-48.

30. A. Shterenlikht and I.C. Howard: Proc. 15th Eur. Conf. of Fracture

(ECF15), KTH, Stockholm, 2004.

31. S.J. Wu and C.L. Davis: Paper presented at the 10th EBSD Conf., Swansea,

United Kingdom, 2003; J. Microsc., 2004, vol. 213, pp. 262-72.

32. S.J. Wu and J.F. Knott: Proc. Conf. on Structural Integrity in the 21st

Century, J. Edwards et al., EMAS Publishing, 2000, pp. 247-55.

METALLURGICAL AND MATERIALS TRANSACTIONS A VOLUME 36A, APRIL 2005—997

33. B. Dutta and C.M. Sellars: Mater. Sci. Technol., 1987, vol. 3, pp. 197-206.

34. A.C. Knessi, G. Posch, C.I. Garcia, and A.J. DeArdo: Proc. Int. Symp.

on Low-Carbon Steels for the 90’s, Pittsburgh, PA, R. Asfahani and

G. Tither, eds., TMS, Warrendale, PA, 1993, pp. 113-19.

35. R.O. Ritchie, J.F. Knott, and J.R. Rice: J. Mech. Phys. Solids. 1973,

vol. 21, pp. 395-410.

36. W.W. Gerberich and E. Kurman: Scripta Metall., 1985, vol. 18,

pp. 295-98.

37. O.M.L. Yahya, F. Borit, R. Piques, and A. Pineau: Fatigue Fracture

Eng. Mater. Struct., 1998, vol. 21 (12), pp. 1485-1502 DEC.

38. P. Hausild, I. Nedbal, C. Berdin, and C. Prioul: Mater. Sci. Eng. A,

2002, vol. 335 (1–2), pp. 164-74.

39. S. Kim, S. Lee, and B.S. Lee: Mater. Sci. Eng. A, 2003, vol. 359 (1–2),

pp. 198-209.

40. M.T. Todinov, M. Novovic, P. Bowen, and J.F. Knott: Mater. Sci.

Eng. A, 2000, vol. 287, pp. 116-24.